塾長(校長)の自由研究
解けそうな問題を見つけよう
成功体験を反芻しよう
バカバカしい自分のアイディアを笑おう。そして、もう一度考えよう
答えが出てから、問題を作ろう
一般化のための一般化を推進し、適用範囲を拡大しよう
制限時間は無制限。気が済むまで考え続けよう
自明なものは、明るすぎて、よく見えない
配線がつながった時が一番楽しい
二兎を追うものは相乗効果を考える
クリストッフェルの記号をMaximaで計算する
Maximaでフリードマン方程式の導出を確認する
Maximaで倒立振り子の微分方程式の導出を確認する
無数の卵形曲線式を生み出す雌鶏変換(パラメータ表示)
f ( x ) は[a b] で狭義の単調増加関数とする。
ただし、f ( ( a + b ) / 2 ) ≠ ( f ( a ) + f ( b ) ) / 2
このとき次の曲線は卵形曲線式となる。
x (θ) = c { f ( ( ( b - a ) cosθ- ( a + b ) ) / 2 ) - ( f ( a ) + f ( b ) ) / 2 }
y (θ) = d sinθ
一般性を損なうことなく運算を容易にするため、a = -1, f ( a ) = -1, b = 1, f ( b ) = 1 とすると上式は
x (θ) = c f ( cosθ)
y (θ) = d sinθ
となる。x = c f ( 0 ) で y (θ) は極値をとる。
f ( x ) の例として f ( -1) = -1, f ( 1 ) = 1となり、f ( 0 ) = t になる2次関数
f1( x ) = - t x2 + x + t
と円弧
f2( x ) = { √( -4 t2 x2 + ( 8 t - 4 t3 ) x + t4 + 4 t2 + 4 ) + t2 - 2 } / ( 2 t )
を挙げておく。いずれも推奨値は c = 1.5、d = 1.1、t = 0.1。
曲線 f ( x ) は、なるべく 直線 y = x に近い形のものを選ぶと良いようです。
あとに出てくるヒステリシス曲線で試したところ、いびつな形になってしまいました。
(2011.05.22)
無数の卵形曲線式を生み出す雌鶏変換(陰関数表示)
f ( x ) は f ( a ) = 0, f ( b ) = 0
区間 [a b] で上に凸とする。
ただし、f ' ( ( a + b ) / 2 ) ≠ 0
このとき次の曲線は区間 [a b]で卵形となる。
y2 = f ( x )
f ( x ) を3次以上の多項式とすると、楕円曲線、超楕円曲線となる。
参考文献:
山本芳彦, "数論入門", 岩波書店
Torsten Sillke, "Egg shaped curves"
http://www.math.uni-bielefeld.de/~sillke/PUZZLES/egg-curves
Jurgen Koller, "Egg Curves Ovals"
http://www.mathematische-basteleien.de/eggcurves.htm
(2011.06.19)
f ( x ) = √( 4a2 x2 + b2 ) - x2 -a2
とすると、カッシーニの卵形曲線となる。
参考文献:
"■[Flash]カッシーニの卵形曲線の描き方", "ガスコン研究所"
http://gascon.cocolog-nifty.com/blog/2009/07/flash-5710.html
(2011.12.30)
座標 (-1, -1), (a, b), (1, 1)を通る関数 (-1<a<1, -1<b<1)をMaximaで計算する
フィッシャーの Z 変換を以下で定義する。
Fisher_Z_transform(r):=log( (1+r) / (1-r) ) / 2 $
上側信頼限界のZ値を以下で定義する。
Zu(r,c):=Fisher_Z_transform(r) + c $
フィッシャーの 逆 Z 変換を以下で定義する。
Inverse_Fisher_Z_transform(Z):=( exp(2*Z) - 1 ) / ( exp(2*Z) + 1 )$
上側信頼限界を以下で定義する。
Upper_confidence_limit(r,a,b):=Inverse_Fisher_Z_transform(Zu(r,Fisher_Z_transform(b)-Fisher_Z_transform(a)))$
以下で定義された関数は表題の条件を満たす。
f(x):=Upper_confidence_limit(x,a,b)$
この関数はパラメータ表示の雌鶏変換のf(x)として
また陰関数表示の雌鶏変換のf(x)の極値のx座標の補正などに使用できる。
参考文献:
大村 平, "統計解析のはなし【改訂版】", 日科技連
青木繁伸, "母相関係数の信頼限界", おしゃべりな部屋 (プラネタリウム,星,植物,熱帯魚,統計学),群馬大学
http://aoki2.si.gunma-u.ac.jp/lecture/Corr/corr3.html
(2011.07.02)
後述の「Maximaで s 個のものを d 日間で処理する計画を立てる」でも使用する。
(2011.11.6)
上式でa = -0.6, b = 0.6 とすると、2割の人口に8割の資源が集中するというパレート曲線になる。
(2011.12.30)
Upper_confidence_limit(x,a,b)を計算すると
- { ( a b - 1 ) x - b + a } / { ( b - a ) x - a b + 1 }
となり
座標 (0, 0), (a, b), (1, 1)を通る関数 (0<a<1, 0<b<1)は
g ( x ) = - ( a - 1 ) b x / { ( b - a ) x - a b + a }
となる。
(2023.12.19)
弁証法的決定表
| 条件 | 現状 | 理想値との相違理由 | 個人的な理想値 | 理由 |
| 条件1 | ○ | ●●のため | × | 似た条件の、条件3に合わせた方が良いかも |
| - | ○ | ■■のため | ||
| 条件2 | × | - | - | |
| 条件3 | × | ◆◆のため | ○ | ■■のため |
個人的な理想値として、背反する結果を同一条件に記入できるため、
矛盾した心情や、仕様確定前のあやふや感、仕様確定後の違和感などを可視化できる。
(2019.05.11)
非周期データをフーリエ級数展開する
p(t)は0≦t≦Tで観測された非周期データとする。
p' (0) = a, p' (T) = b と置く。
q(t) = p(t) - 2 a T sin(πt / ( 2 T ) ) / π - 2 b T cos(πt / ( 2 T ) ) / π
とすると、q' (0) = q' (T) = 0 となる。
q(0) = c, q(T) = d と置く。
r(t) = q(t) - ( c - d ) cos(πt / T ) / 2 - ( c + d ) / 2
とすると、r(0) = r(T) = r' (0) = r' (T) = 0 となる。
よって、r(t)を0≦t≦Tでフーリエ級数展開したものを、s(t)とすると
p(t) = s(t) + ( c - d ) cos(πt / T ) / 2 + ( c + d ) / 2 + 2 a T sin(πt / ( 2 T ) ) / π + 2 b T cos(πt / ( 2 T ) ) / π
(2020.06.24)
逆関数の折れ線近似関数
x0≦x≦xn における狭義の単調増加関数f (x) の折れ線近似関数は
x0<x1<…<xnとすると
g (x) = ( |x| - |x - 1| + 1 ) / 2
h (x) = f (x0) +Σ{ i = 1~n } ( f ( xi ) - f ( xi-1) ) g ( ( x - xi-1) / ( xi - xi-1 ) )
となり、f (x)の逆関数の折れ線近似関数は
j (x) = x0 + Σ{ i = 1~n } ( xi - xi-1) g ( ( x - f ( xi-1) ) / ( f (xi) - f (xi-1) ) )
f (x0)≦x≦f (xn)
となる。
f (x)が狭義の単調減少関数とすると
その逆関数の折れ線近似関数は
k (x) = xn +Σ{ i = 0 ~ n-1 } ( xi - xi+1) g ( ( x - f ( xi+1) ) / ( f (xi) - f ( xi+1) ) )
f (xn)≦x≦f (x0)
となる。
この折れ線近似関数の利点は
・逆関数を数学的に求めることができなくても、逆関数の近似関数を簡単に作れる
・方程式が解ける関数を持たない表計算ソフトでも、解の近似値を簡単に計算できる
欠点は
・線形近似のため科学技術計算には使えない→精度の必要ないビジネス計算用
・区間外で使ってはいけない
逆関数の近似関数の精度を上げるには
・計算資源が許す限りnを大きくする
f (x)の曲率の大きいところにxiを多めに配置する
(2016.02.07)
・ x = f -1 ( f (x) ) であるから逆関数の近似関数は補正しやすい
y' = j ( f (y) ) からy≒p(y')となるp(x)を作ると、補正された逆関数の近似関数は
j ' (x) = p ( j (x) )
となる
z' = j ' ( f (z) ) からz≒p' (z')となるp' (x)を作ると、補正された逆関数の近似関数は
j ' ' (x) = p ' ( j ' (x) )
となる
このように、計算資源が許す限り、補正を繰り返すことができる
(2017.08.05)
折れ線近似関数の積分
L≦x≦M における関数f0 (x) の折れ線近似関数が
g (x) = ( |x| - |x - 1| + 1 ) / 2
h0 (x) = f0 (x0) +Σ{ i = 1~n } ( f0 ( xi ) - f0 ( xi-1 ) ) g ( ( x - xi-1) / ( xi - xi-1 ) )
L=x0<x1<…<xn=M
であるとき、その積分は
H0(x) = f0 (x0) ( x - x0) + ( f0(xn) - f0(x0) ) x / 2 +Σ{ i = 1~n } { ( f0 (xi-1) - f0 (xi) ) ( ( x - xi ) | x - xi | - ( x - xi-1) | x - xi-1 | ) / ( 4 | xi - xi-1 | ) - ( xi + xi-1 ) f0(xi) / 4 }
となる
L≦x≦M における関数f1(x) = f0 (x) - h0(x)の折れ線近似関数が
h1 (x) = Σ{ i = 1~m } ( f1 ( yi ) - f1 ( yi-1 ) ) g ( ( x - yi-1) / ( yi - yi-1 ) )
L=y0<y1<…<ym=M
であるとき、その積分は
H1(x) = ( f1(ym) - f1(y0) ) x / 2 +Σ{ i = 1~m } { ( f1 (yi-1) - f1 (yi) ) ( ( x - yi ) | x - yi | - ( x - yi-1) | x - yi-1 | ) / ( 4 | yi - yi-1 | ) - ( yi + yi-1 ) f1(yi) / 4 }
となる
∫[L x] f0 (t) dt ≒ H0(x) + H1(x)
xi 、yi は等間隔に並んでいる必要はなく xi = yi である必要もない
以下同様に補正することができる
∫[L x] f0 (t) dt ≒ H0(x) + H1(x) + H2(x) + …
(2016.02.08)
リトルの公式を算数の問題に帰着させる
平均到着率を1分間に待ち行列に入ってくる平均人数、
平均出発率を1分間に待ち行列から出ていく平均人数とする。
待ち行列に人が並び始めてから待ち行列が無くなるまでの間の、平均到着率と平均出発率は等しいので
これをリトルの公式に代入すると
待ち行列の平均待ち時間=待ち行列の人数/平均出発率
となる。
待ち行列を動画に記録し逆再生したものにリトルの公式を適用すれば同じ結論を得る。
参考文献:北岡正敏, "例題でわかる待ち行列理論入門", 日本理工出版会
(2013.05.03)
集合の類似度
|X| ≦ |Y|とする。
集合の類似度r を|X|と|Y|だけで考えた場合
|X| = |Y|の場合、r = 1
|X| < |Y|の場合、0 ≦ r < 1
となるはずだが、
Simson係数sは、
s = |X∩Y| / |X|
で、XとX∩Yを固定した場合、|Y|の大きさによらず、sは定数となる。
特に、X⊆Yの場合、共に s = 1 となり、集合の類似度として不適切である。
そこで、sに|X| / |Y|を掛けると
t = |X∩Y| / |Y|
を得る。
t は、Jaccard係数の近似値であり、X⊆Yの場合、Jaccard係数に一致する。
Simson係数が集合の類似度でないとすると、他にどういう意味があるのかというと、
無作為にx∈Xを選んだとき、x∈Yになる確率、つまり
XならばY ( X ⇒ Y ) が成立する確度を表す。
そこで、sに
YならばX ( Y ⇒ X ) が成立する確度を表すt を掛けると
c2 = st
を得る。ここでcはCosine係数である。
X ⇒ Y は、X∩¬Y = Φであり、Y ⇒ X は、¬X∩Y = Φであるから、
X ⇒ Y が成立する確度は、1 - |X∩¬Y| / |X| = 1 - ( |X| - |X∩Y| ) / |X| = s
Y ⇒ X が成立する確度は、1 - |¬X∩Y| / |Y| = 1 - ( |Y| - |X∩Y| ) / |Y| = t
であり、
X = Y が成立する確度は、s t となる。
参考文献:金子冴, "【技術解説】集合の類似度(Jaccard係数,Dice係数,Simpson係数)", ミエルカAIメディア
"商品分析の手法(ABC分析、アソシエーション分析)", 株式会社ALBERT
(2020.08.01)
条件付き確率で多変量解析をする
原因1と原因2が独立事象とすると、
P(結果 | 原因1 ∩ 原因2)
= P(結果 ∩ 原因1 ∩ 原因2) / P(原因1 ∩ 原因2)
= { P(結果 ∩ 原因1) / P(原因1) } { P(結果 ∩ 原因2) / P(原因2) }
= { n(結果 ∩ 原因1) / n(原因1) } { n(結果 ∩ 原因2) / n(原因2) }
ここで、n(原因1) = 0 の場合は、原因1 = 結果 とする。
また、P(結果) ≧ 0.5 となるようにするとよい。
(2017.12.03)
Windowsフォルダのショートカットを読み取り専用にする方法
フォルダのショートカットを右クリック→プロパティ→ショートカットタブ
→リンク先の先頭に
EXPLORER
を追記する(EXPLORERの後ろに半角スペースを入れる)。
→OKボタンを押す。
このショートカットの上に、ファイルやフォルダを誤ってドロップしても、ドキュメントフォルダが開くだけで、
ファイルやフォルダがコピーされたり、移動されたりすることがなく、
ダブルクリックすれば、リンク先のフォルダを開くことができる。
(2020.06.29)
オブジェクト指向のメッセージは、メソッドではなくgoto文で実装すべきだった?
メッセージパッシングは
1.オブジェクト間でメッセージを交換しながら処理進める。
2.メッセージの送り先のオブジェクトに実行制御を委譲する。
の2つでワンセットである必要があるのではないかと思う。
であるとすれば、送信元に制御が返って来るメソッドよりも、goto文の方が、ふさわしいのでは、ないだろうか?
メッセージをメソッドで実装しているオブジェクト指向言語で、擬似的に、このメッセージパッシングを実現するには、
メソッドを呼び出した直後に、値を返さないreturn文を実行する必要がある(ただし、callスタックを浪費してしまう)。
(2017.07.27)
WSH JScript で、callスタックの浪費を気にせずにメッセージパッシングをするサンプル
以下のサンプルは、リーダーとライターが互いにメッセージを送って、Hello Worldを出力します。
リーダーは、デバイスの仕様(という想定)により、1文字づつ逆順に送信します。
Messageオブジェクトを返すメソッド間であれば、callスタックを浪費することなく、メッセージを送信し合うことができます。
//---------------
// HelloWorld.js
//---------------
//メッセージオブジェクト
var Message = function(func,parameter) {
var _function = func; //メッセージ
var _parameter = parameter; //パラメータ
//メッセージを送る
this.sendMessage = function() {
return _function(_parameter);
}
}
//リーダー
var Reader = function(str) {
var _str = str; //文字列
var _cnt = str.length - 1; //カウンタ
//文字の送信要求を受け付ける
this.wantChar = function(args) {
if(_cnt >= 0) {
//メッセージで文字を送る(デバイスの仕様により逆順に送る)
return new Message(args.sender.send,{ch:_str.charAt(_cnt--)});
}
//全て送ったので、出力するようにメッセージを送る
return new Message(args.sender.write);
}
}
//ライター
var Writer = function(rd) {
var _rd = rd; //メッセージ送信先リーダー
var _str = ""; //文字列バッファー
var _me = this; //自己インスタンス
//リーダーから文字を受け取る
this.send = function(args) {
//バッファーに書く
_str += args.ch;
//リーダーに文字の送信要求をメッセージで送る
return new Message(_rd.wantChar,{sender:_me});
}
//出力メッセージを受け付ける
this.write = function() {
var str = "";
var i;
//バッファーに逆順に格納されている文字列を正順にする
for(i=_str.length - 1;i>=0;i--) {
str += _str.charAt(i);
}
//文字列を出力する
WScript.Echo(str);
//終了メッセージを送る
return null;
}
}
//リーダーとライターを生成する
var wr = new Writer(new Reader("Hello World"));
//最初の送信メッセージを生成する
var ms = new Message(wr.send,{ch:""});
//主処理
while(ms != null) {
ms = ms.sendMessage();
}
主処理は、プログラムカウンタのないCPUとして振る舞っている。
つまり、メッセージとはgoto文付きの命令セットである。
参考文献:山田好寛, "改訂新版 JavaScript 本格入門", 技術評論社
(2017.07.29)
WSH JScript で、ハノイの塔問題を解く
以下のサンプルは、一見すると再帰で解いているように見えますが、実際はループ処理をしています。(サイキック・ループ処理)
メッセージキューのスタックを使い、callスタックを、ほとんど消費しません。
//---------------
// hanoi.js
//---------------
var DISK_N = 4; //円盤の枚数
//メッセージキューのスタック
var MessageQueueStack = function() {
var _MQ = []; //メッセージキュー
var _stack = []; //スタック
//メッセージオブジェクト
var _Message = function(func,parameter) {
var _function = func; //メッセージ
var _parameter = parameter;
//パラメータ
//メッセージを送る
this.sendMessage = function()
{
return
_function(_parameter);
}
}
//メッセージ(func,parameter)をキューに登録する
this.queuePush = function(func,parameter) {
_MQ.push(new _Message(func,parameter));
}
//スタックにメッセージキューを積む
var _stackPush = function() {
_stack = _MQ.concat(_stack);
//メッセージキューを解放
_MQ = [];
}
//主処理
this.run = function() {
//最初のメッセージキューをスタックに積む
_stackPush();
//主処理
while(_stack.length >
0) {
//スタックの一番上のメッセージを取り出しメッセージを送る
_stack.shift().sendMessage();
//スタックにメッセージキューを積む
_stackPush();
}
}
}
//メッセージキューのスタックをインスタンス化
var MQS = new MessageQueueStack();
//ライタークラス
var Writer = function() {
var _str = []; //出力バッファー
var _line = ""; //行バッファー
//行バッファーへ書き込む
this.Write = function(args) {
_line += args.str;
}
//改行
this.newLine = function() {
//行バッファーから出力バッファーへ書き込む
_str.push(_line);
//行バッファーを解放する
_line = "";
}
//出力
this.outPut = function() {
var fs = new ActiveXObject("Scripting.FileSystemObject");
var sh = WScript.CreateObject("WScript.Shell");
//出力ファイルのフルパス名を取得する
var fnm = fs.getParentFolderName(WScript.ScriptFullName)
+ "\\hanoi.txt";
//同じ名前のファイルがある場合はメッセージを出す
if(fs.FileExists(fnm))
{
if(2==sh.Popup("同じフォルダにhanoi.txtファイルがあります。上書きしますか?",
0, "hanoi.js", 1)) {
WScript.Quit(1);
}
}
//同じ名前のフォルダがある場合はメッセージを出す
if(fs.FolderExists(fnm))
{
WScript.Echo("同じフォルダにhanoi.txtフォルダがあり、出力できません。");
WScript.Quit(2);
}
//出力ファイルを上書きモードで開き、出力する
var otf = fs.OpenTextFile(fnm,
2, true);
var j = -1;
for(j in _str) {
otf.WriteLine(_str[j]);
}
//出力ファイルを閉じる
otf.Close();
WScript.Quit(0);
}
}
//ライタークラスをインスタンス化する
var wr = new Writer();
var A_AXIS = 0; //A軸
var B_AXIS = 1; //B軸
var C_AXIS = 2; //C軸
//ハノイの塔クラス
var HanoiTower = function(n) {
var _axisName = ["A軸","B軸","C軸"];
//軸名
var _axis = [[],[],[]]; //軸
//A軸に円盤をセットする
var _i;
for(_i = n ; _i > 0 ; _i--) {
_axis[A_AXIS].push(_i);
}
_showDiskState();
//円盤の状態を表示する
function _showDiskState() {
var j = -1;
var k = -1;
for(j in _axis) {
MQS.queuePush(wr.Write,{str:_axisName[j]
+ ":"});
for(k
in _axis[j]) {
MQS.queuePush(wr.Write,{str:((k
> 0) ? "," : "") + _axis[j][k]});
}
MQS.queuePush(wr.newLine);
}
}
//円盤を移動する
this.move = function(args) {
//fromからdestへ円盤を移動する
_axis[args.dest].push(_axis[args.from].pop());
//移動したことを出力するメッセージを設定する
MQS.queuePush(wr.Write,{str:">>>>>>>>>>"
+ _axisName[args.from] + "から" + _axisName[args.dest] + "へ"});
MQS.queuePush(wr.newLine);
//円盤の状態を表示する
_showDiskState();
}
}
//ハノイの塔クラスをインスタンス化する
var ht = new HanoiTower(DISK_N);
//ハノイの塔を解く
var hanoi = function(args) {
//再帰処理と同じ順にメッセージキューへ入れる
if(args.n >= 2) MQS.queuePush(hanoi,{n:args.n-1,
from:args.from, work:args.dest, dest:args.work});
MQS.queuePush(ht.move,{from:args.from, dest:args.dest});
if(args.n >= 2) MQS.queuePush(hanoi,{n:args.n-1,
from:args.work, work:args.from, dest:args.dest});
}
//ハノイの塔を解くメッセージを設定する
MQS.queuePush(hanoi,{n:DISK_N, from:A_AXIS, work:B_AXIS, dest:C_AXIS});
//出力メッセージを設定する
MQS.queuePush(wr.outPut);
//主処理開始
MQS.run();
参考文献:kymats, "ハノイの塔を攻略せよ!", Windowsプログラミング研究所, http://www13.plala.or.jp/kymats/study/C++/Hanoi/Hanoi.html
羽山
博, "WSH クイックリファレンス 第2版", オライリー・ジャパン
(2017.09.02)
WSH JScriptでHaskell風無限リストプログラミングを楽しむためのライブラリ
無限リストの概念がない言語では、オブジェクトやクロージャーなどで内部状態を持たせた、引数のない関数(メソッド)を無限リストの代用とすることができる。
定数関数は、同じ値が無限個続く無限リストとみなす。
有限リストは有限個の値と無限個の非値(ここではnullを使用)からなる無限リストで表現する。(nullの有限列は使用しない)
ただし、Haskellの無限リストと違い、代入でリストのコピーは作れない。
下記のライブラリでは無限リスト(引数のない関数)を無限リストオブジェクトに格納し、メソッドチェーンによりパイプライン風に処理できるようにしています。
//Haskell風に無限リストを扱うライブラリー
function InfiniteListLibrary() {
var thi = this;
this.zip = function( iList ) { return this.zipPrototype( iList, thi
); };
this.map = function( func ) { return function( thist ) { return thi.pure( function() { var item = thist.head(); return ( item == null )? null : func( item ); } ); }; };
this.last = function() { return this.lastPrototype( this ); };
this.take = function( n ) { return function( thist ) { return thist.b(
thi.zip( thi.countDown( n ) ) ).b( thi.takeWhile( function( item ) { return
( item.snd > 0 ); } ) ).b( thi.map( function( item ) { return item.fst;
} ) ); }; };
this.drop = function( n ) { return function( thist ) { return thist.b( thi.zip( thi.countDown( n ) ) ).b( thi.dropWhile( function( item ) { return ( item.snd > 0 ); } ) ).b( thi.map( function( item ) { return item.fst; } ) ); }; };
//無限リストを無限リストオブジェクトに格納する
this.pure = function( list ) { return new InfiniteList( list ); };
//文字列無限リストオブジェクトを改行で分割し文字列無限リストオブジェクトの無限リストオブジェクトを作る
this.lines = function() { return this.linesPrototype( this ); };
this.unzip = function() { return this.unzipPrototype( this ); };
//Haskellのlengthに相当
this.count = function() { return function( thist ) { return thist.b(
thi.foldlP( function( s ) { return ( s + 1 ); }, 0 ) ); }; };
//Haskellのfoldl'に相当
this.foldlP = function( func, init ) { return function( thist ) { return thist.b( thi.scanlP( func, init ) ).b( thi.last() ); }; };
this.filter = function( p ) { return function( thist ) { return thi.pure(
function() { return thist.b( thi.filterPrototype( p ) ); } ); }; };
//Haskellのscanl'に相当
this.scanlP = function( func, init ) { return this.scanlPPrototype( func, init, this ); };
//Haskellのscanl1'に相当
this.scanl1P = function( func ) { return function( thist ) { return
thist.b( thi.scanlP( func, thist.head() ) ); }; };
//定数の無限リストオブジェクトを作る
this.constant = function( n ) { return thi.pure( function() { return
n; } ); };
//文字列無限リストオブジェクトをString型に変換する
this.toString = function() { return function( thist ) { return thist.b( thi.foldlP( function( s, item ) {return (s+item);}, '' ) ); }; };
this.plusPlus = function( iList ) { return this.plusPlusPrototype(
iList, thi ); };
//0までカウントダウン後0であり続ける無限リストオブジェクトを作る
this.countDown = function( n ) { return this.constant( 1 ).b( thi.scanlP( function( s, a ) { return ( s > 0 ? 1 : 0 )*( s - a ); }, n ) ); };
//Haskellの[n..]に相当
this.enumerate = function( n ) { return this.constant( 1 ).b( thi.scanlP(
function( s, a ) { return s + a; }, n ) ); };
//takeWhileとdropWhileの補助メソッド
this.whileList = function( n ) { return this.whileListPrototype( n, this ); };
this.takeWhile = function( p ) { return function( thist ) { return
thist.b( thi.whileList( p ) ).b( thi.map( function( item ) { return ( item.snd
) ? item.fst : null; } ) ).b( thi.plusPlus( thi.constant( null ) ) ); };
};
this.lookup = function( key ) { return function( thist ) { return
thist.b( thi.filter( function( item ) { return ( item.fst == key ); } )
).b( thi.map( function( item ) { return item.snd; } ) ).head(); }; };
this.dropWhile = function( p ) { return function( thist ) { return thist.b( thi.whileList( p ) ).b( thi.filter( function( item ) { return !item.snd; } ) ).b( thi.map( function( item ) { return item.fst; } ) ); }; };
//String型と配列を無限リストオブジェクトを変換する
this.convertIntoInfiniteList = function( arr ) { return this.convertIntoInfiniteListPrototype(
arr, thi ); };
//無限リストオブジェクトを配列に変換する
this.convertInfiniteListIntoArray = function() { return function(
thist ) { return thist.b( thi.foldlP( function( s, item ) { s.push( item
); return s; }, [] ) ); }; };
InfiniteList.prototype = {
//無限リストオブジェクトにライブラリーメソッドを適用するメソッド
b : function( func ) { return func( new InfiniteList( this.list
) ); }
,
//無限リストオブジェクトから先頭の要素を取り出す
head : function() { return this.list(); }
};
//無限リストオブジェクト
function InfiniteList( list ) {
this.list = list;
}
};
InfiniteListLibrary.prototype = {
uncons : function() { return function( thist ) { return { fst: thist.head(),
snd: thist }; }; }
,
//無限リストオブジェクトの無限リストオブジェクトをmapするときに使用する
receiveIL : function( func ) { return function( il ) { return il.b( func ); }; }
,
//以下のメソッドは接尾辞がPrototypeでないメソッドの補助メソッド
whileListPrototype : function( p, thi ) {
return function( thist ) { return thist.b( thi.map( function(
item ) { return { fst: item, snd: item != null && p( item ) } ;
} ) ).b( thi.scanl1P( function( s, item ) { return { fst: item.fst, snd:
( s.snd && item.snd) } ; } ) ); };
}
,
lastPrototype : function( thi ) {
return function( thist ) {
var item = thist.b( thi.map( function( item ) { return
{ fst: item, snd: true }; } ) ).b( thi.unzip() );
var list = item.snd.b( thi.drop( 1 ) ).b( thi.plusPlus(
thi.constant( null ).b( thi.scanlP( function( s, item ) { return item;
}, false ) ) ) ).b( thi.zip( item.fst ) ).b( thi.dropWhile( function( item
) { return item.fst; } ) );
return list.b( thi.map( function( item ) { return item.snd;
} ) ).head();
};
}
,
plusPlusPrototype : function( iList, thi ) {
return function( thist ) { return thi.pure( plusPlus( thist,
iList ) ); };
function plusPlus( list1, list2 ) {
//list1が消費されたらwListをlist2に置き換える
var wList = thi.pure( function() { var item = list1.head();
return ( item == null ) ? ( function() { var it = list2.head(); wList =
list2; return it; } )() : item; } );
return function() { return wList.head(); };
}
}
,
scanlPPrototype : function( func, init, thi ) {
return function( thist ) { return thi.pure( scanlP( func, init
, thist ) ); };
function scanlP( func, init, list ) {
var s = init;
//wListは最初の1回だけ違う
var wList = ( thi.pure( function() { wList = list.b(
thi.map( function( item ) { s = func( s, item ); return s; } ) ); return
init; } ) );
return function() { return wList.head(); };
}
}
,
zipPrototype : function( iList, thi ) {
return function( thist ) { return thi.pure( zip( thist, iList
) ); };
function zip( list1, list2 ) {
return function() {
var l1 = list1.head();
var l2 = list2.head();
return ( (l1==null) || (l2==null) ) ? null : {
fst:l1, snd:l2 };
};
}
}
,
convertIntoInfiniteListPrototype : function( arr, thi ) {
var ss = ( Object.prototype.toString.call(arr).slice(8, -1).toLowerCase()!='string'
? function() {return new Enumerator(arr);} : function() {return new EnumeratorStr(arr);}
)();
return thi.pure( function() { return ( ss.atEnd() ? function()
{ return null; } : function() {var a = ss.item();ss.moveNext();return a;}
)(); } );
//String型をEnumeratorにする
function EnumeratorStr(arr) {
var cnt = 0;
this.item = function() { return arr.charAt(cnt); };
this.atEnd = function() { return (cnt >= arr.length);
};
this.moveNext = function() { cnt++; };
}
}
,
filterPrototype : function( p ) {
return function( thist ) { return until( p, thist ); };
function until( p, list ) {
var item;
//ループエンジン
while(true) {
item = list.head();
if( item == null ) return null;
if( p( item ) ) break;
}
return item;
}
}
,
unzipPrototype : function( thi ) {
return function( thist ) {
var fst = [];
var snd = [];
return {
fst: thi.pure( function() {
if( fst.length > 0 ) return fst.shift();
var item = thist.head();
if( item == null ) return null;
snd.push( item.snd );
return item.fst;
} )
, snd: thi.pure( function() {
if( snd.length > 0 ) return snd.shift();
var item = thist.head();
if( item == null ) return null;
fst.push( item.fst );
return item.snd;
} )
};
};
}
,
linesPrototype : function( thi ) {
return function( thist ) { return thi.pure( lines( thist )
); };
function lines( list ) {
var n = 0;
var mb = new ManageBuffer();
return function() {
if( n > 0 ) if( mb.linefeed() ) return null;
return thi.pure( function() { return mb.getChar(
n++ ); } );
};
//バッファー管理クラス
function ManageBuffer() {
var _buff = new Map();
var wList1 = list.b( preloading() ).b( thi.drop(
1 ) );
var wList2 = wList1.b( thi.takeWhile( isNotLF )
).b( thi.map( function( item ) { return item.snd; } ) );
//次の行を取得する。現在行の読み取りが終わっていない場合バッファーに入れる
this.linefeed = function() {
var arr = wList2.b( thi.convertInfiniteListIntoArray()
);
if( arr.length > 0 ) _buff.set( n-1, arr
);
var it = wList1.b( thi.map( function( item
) { return item.fst; } ) ).head();
wList2 = wList1.b( thi.takeWhile( isNotLF
) ).b( thi.map( function( item ) { return item.snd; } ) );
return (it==null);
};
//指定した行から1文字取り出す
this.getChar = function( idx ) {
var arr = _buff.get( idx );
if( arr == null ) return ( idx + 1 == n )?
wList2.head() : null;
var it = null;
if( arr.length > 0 ) it = arr.shift();
if( arr.length == 0 ) _buff.erase( idx );
return it;
};
function isNotLF( item ) { return ( item.snd !=
null && !( item.snd == '\r' && item.fst == '\n' ) ); }
function preloading() {
return function( thist ) {
var list = thist.b( thi.plusPlus( thi.constant(
null ).b( thi.scanlP( function( s, it ) { return it; }, ' ' ) ) ) ).b(
thi.map( function( ite ) { return { fst:ite, snd:null }; } ) );
return list.b( thi.scanl1P( function( s,
it ) { return { fst:it.fst, snd:s.fst }; } ) );
};
}
//JavaScriptのMapに相当
function Map() {
var _arr = [];
this.get = function( key ) { return thi.convertIntoInfiniteList(
_arr ).b( thi.lookup( key ) ); };
this.set = function( key, val ) { return keyMatchIf(
key, function( i ) { _arr[i].snd = val; }, function() { _arr.push( { fst:key,
snd:val } ); } ); };
//JavaScriptのdeleteに相当
this.erase = function( key ) { return keyMatchIf(
key, function( i ) { _arr.splice( i, 1 ); }, function() {} ); };
function keyMatchIf( key, same, mismatch ) {
var item = thi.convertIntoInfiniteList( _arr
).b( thi.zip( thi.enumerate( 0 ) ) ).b( thi.filter( function( it ) { return
( it.fst.fst !== key ) } ) ).head();
return ( item == null ) ? ( function() {
mismatch(); return null; } )() : same( item.snd );
}
}
};
}
}
}
参考文献: Miran Lipovaca,"すごいHaskellたのしく学ぼう!",オーム社
重城良国,"Haskell
教養としての関数型プログラミング",秀和システム
@HelloRusk,"GHC.List を読んで Haskell のリスト操作をまとめた",Qiita
@kwatch,"【長編ポエム】関数型言語が分からんお前でもPythonなら分かるやろ",Qiita
@ozwk,"ループを再帰関数にする考え方",Qiita
(2020.10.24)
Ver.2公開に伴い上記コードは今後削除されます。
//Haskell風に無限リストを扱うライブラリー(Ver.2)
function InfiniteListLibrary() {
var thi = this;
this.map = function( func ) { return function( thst ) { return function()
{ if( thst ) { var item = thst(); if( item == null ) { thst = undefined;
return null; }; return func( item ); }; return null; }; }; };
this.zip = function( iList ) { return function( thst ) { return thi.pipeline( thst, [ thi.map( function( it1 ) { if( !iList ) return null; var it2 = iList(); if( it2 == null ) { iList = undefined; return null }; return { fst: it1 , snd: it2 }; } ) ] ); }; };
this.any = function( p ) { return function( thst ) { return thi.pipeline(
thst, [ thi.filter( p ), thi.head() ] ) == null ? false : true; }; };
this.last = function() { return function( thst ) { return thi.pipeline(
thst, [ thi.biGram(), thi.dropWhile( function( item ) { return ( item.snd
!= null ); } ), thi.map( function( item ) { return item.fst; } ), thi.head()
] ); }; };
this.take = function( n ) { return function( thst ) { return thi.pipeline( thst, [ thi.countDownSubscript( n ), thi.takeWhile( function( item ) { return ( item.snd > 0 ); } ), thi.map( function( item ) { return item.fst; } ) ] ); }; };
this.drop = function( n ) { return function( thst ) { return thi.pipeline(
thst, [ thi.countDownSubscript( n ), thi.dropWhile( function( item ) {
return ( item.snd > 0 ); } ), thi.map( function( item ) { return item.fst;
} ) ] ); }; };
this.cons = function( n ) { return function( thst ) { return function()
{ if( n != null ) { var w = n; n = null; return w; }; if( thst ) { var
item = thst(); if( item != null ) return item; thst = undefined; }; return
null; }; }; };
//無限リストから先頭の要素を取り出し不要になった無限リストを開放する
this.head = function() { return function( thst ) { if( thst ) { var
item = thst(); if( item == null ) thst = undefined; return item; }; return
null; }; };
this.mapM_ = function( func ) { return function( thst ) { thi.pipeline(
thst, [ thi.map( func ), thi.last() ] ); return null; }; };
//文字列無限リストを改行で分割し文字列無限リストの無限リストを作る
this.lines = function() { return this.linesPrototype( this ); };
this.unzip = function() { return this.unzipPrototype( this ); };
//Haskellのlengthに相当
this.count = function() { return function( thst ) { return thi.pipeline(
thst, [ thi.foldlP( function( s ) { return ( s + 1 ); }, 0 ) ] ); }; };
this.concat = function() { return function( thst ) { return thi.pipeline(
thst, [ thi.concatFilter( function( item ) { return true; } ) ] ); }; };
//Haskellのfoldl'に相当
this.foldlP = function( func, init ) { return function( thst ) {
return thi.pipeline( thst, [ thi.scanlP( func, init ), thi.last() ] );
}; };
this.filter = function( p ) { return function( thst ) { return thi.pipeline(
thi.constant( null ), [ thi.cons( thst ), thi.concatFilter( p ) ] ); };
};
//Haskellのscanl'に相当
this.scanlP = function( func, i ) { return function( thst ) { return
thi.pipeline( thi.constant( null ), [ thi.cons( i ), thi.plusPlus( thi.pipeline(
thst, [ thi.map( function( item ) { i = func( i, item ); return i; } )
] ) ) ] ) }; };
this.lookup = function( key ) { return function( thst ) { return
thi.pipeline( thst, [ thi.filter( function( item ) { return ( item.fst
== key ); } ), thi.map( function( item ) { return item.snd; } ), thi.head()
] ); }; };
//bi-gram
this.biGram = function() { return this.biGramPrototype( this ); };
this.uncons = function() { return function( thst ) { return { fst:
thst(), snd: thst }; }; };
//Haskellのscanl1'に相当
this.scanl1P = function( func ) { return function( thst ) { return
thi.pipeline( thst, [ thi.scanlP( func, thst() ) ] ); }; };
//定数の無限リストを作る
this.constant = function( n ) { return function() { return n; }; };
//文字列無限リストをString型に変換する
this.toString = function() { return function( thst ) { return thi.pipeline(
thst, [ thi.foldlP( function( s, item ) {return (s+item);}, '' ) ] ); };
};
//Haskellの(++)に相当
this.plusPlus = function( iList ) { return function( thst) { return
thi.pipeline( thi.constant( null ), [ thi.cons( iList ), thi.cons( thst
), thi.concat() ] ); }; };
//無限リストに対し配列に入った関数を順に適用する
this.pipeline = function( ret, arr ) { return thi.pipelinePrototype(
ret, arr, thi ); };
//Haskellの[n..]に相当
this.enumerate = function( n ) { return thi.pipeline( this.constant(
1 ), [ thi.scanlP( function( s, a ) { return s + a; }, n ) ] ); };
//takeWhileとdropWhileの補助メソッド
this.whileList = function( n ) { return this.whileListPrototype(
n, this ); };
this.takeWhile = function( p ) { return function( thst ) { return
thi.pipeline( thst, [ thi.whileList( p ), thi.map( function( item ) { return
( item.snd ) ? item.fst : null; } ) ] ); }; };
this.dropWhile = function( p ) { return function( thst ) { return thi.pipeline( thst, [ thi.whileList( p ), thi.filter( function( item ) { return !item.snd; } ), thi.map( function( item ) { return item.fst; } ) ] ); }; };
//無限リストに入った無限リストをmapするときに使用する
this.receiveIL = function( func ) { return function( il ) { return
thi.pipeline( il, [ func ] ); }; };
//concatしてfilterする
this.concatFilter = function( p ) { return function( thst ) { return
thi.loopEngine( thst, thst(), p, function() { return null; } ); }; };
//カウントダウン添え字を付ける
this.countDownSubscript = function( n ) { return function( thst ) { return thi.pipeline( thst, [ thi.map( function( item ) { return { fst: item, snd: n }; } ), thi.scanl1P( function( s, item ) { return { fst: item.fst, snd: s.snd - 1 }; } ) ] ); }; };
//String型と配列を無限リストに変換する
this.convertIntoInfiniteList = function( arr ) { return this.convertIntoInfiniteListPrototype(
( Object.prototype.toString.call( arr ).slice( 8, -1 ).toLowerCase() ==
'string' ) ? arr.split("") : arr, thi ); };
//無限リストを配列に変換する
this.convertInfiniteListIntoArray = function() { return function(
thst ) { return thi.pipeline( thst, [ thi.foldlP( function( s, item ) {
s.push( item ); return s; }, [] ) ] ); }; };
};
InfiniteListLibrary.prototype = {
//ループエンジン
loopEngine : function( liss, lis, pp, getRet ) {
return function() {
if( !liss || !lis ) return null;
while( true ) {
var item = lis();
if( item == null ) {
lis = liss();
if( !lis ) {
lis = undefined;
liss = undefined;
return getRet();
}
} else {
if( pp( item ) ) return item;
}
}
};
}
,
//以下のメソッドは接尾辞がPrototypeでないメソッドの補助メソッド
convertIntoInfiniteListPrototype : function( arr, thi ) { return
thi.pipeline( thi.constant( arr ), [ thi.map( function( s ) { if( s &&
s.length ) return s.shift(); arr = undefined; return null; } ) ] ); }
,
whileListPrototype : function( p, thi ) {
return function( thst ) { return thi.pipeline( thst, [ thi.map(
function( item ) { return { fst: item, snd: item != null && p(
item ) } ; } ), thi.scanl1P( function( s, item ) { return { fst: item.fst,
snd: ( s.snd && item.snd) } ; } ) ] ); };
}
,
biGramPrototype : function( thi ) {
return function( thst ) {
var lis = thi.pipeline( thi.constant( null ), [ thi.cons(
{ fst:null, snd:null } ) ] );
return thi.pipeline( thst, [ thi.map( function( ite )
{ return { fst:null, snd:ite }; } ), thi.plusPlus( lis ), thi.scanl1P(
function( s, it ) { return { fst:s.snd, snd:it.snd }; } ), thi.drop( 1
) ] );
};
}
,
pipelinePrototype : function( ret, arr, thi ) {
if( !arr || arr.length == 0 ) return li;
var lists = toList( [ toList( arr ) ] );
var list = ( lists )();
if( !lists || !list ) return null;
return ( thi.loopEngine( lists, list, function( item ) { ret
= item( ret ); return false; }, function() { return ret; } ) )();
function toList( arr ) { return function() { return arr.shift();
}; }
}
,
unzipPrototype : function( thi ) {
return function( thst ) {
var aObj = { fst:[], snd:[] };
return { fst: function() { return unz( 'fst', 'snd' );
}, snd: function() { return unz( 'snd', 'fst' ); } };
function unz( lv, rv ) {
if( aObj[lv].length > 0 ) return aObj[lv].shift();
if( !thst ) {
if( aObj && !aObj[rv].length ) aObj
= undefined;
return null;
}
var item = thst();
if( item == null ) {
thst = undefined;
return null;
}
aObj[rv].push( item[rv] );
return item[lv];
}
};
}
,
linesPrototype : function( thi ) {
return function( thst ) { return lines( thst ); };
function lines( list ) {
var n = 0;
var mb = new manageBuffer();
return function() {
if( !mb ) return null;
if( n > 0 && mb.linefeed() ) {
if( mb.isReleasable() ) mb = undefined;
return null;
}
var idx = n++;
return function() { return mb ? mb.getChar( idx
) : null; };
};
//バッファー管理クラス
function manageBuffer() {
var localVar = { buff: new Map(), list: [ null,
null ] };
localVar.list[0] = thi.pipeline( list, [ thi.biGram()
] );
localVar.list[1] = thi.pipeline( localVar.list[0],
[ thi.takeWhile( isNotLF ), thi.map( function( item ) { return item.fst;
} ) ] );
//次の行を取得する。現在行の読み取りが終わっていない場合バッファーに入れる
this.linefeed = function() {
if( !localVar || !localVar.list ) return true;
var arr = thi.pipeline( localVar.list[1], [ thi.convertInfiniteListIntoArray()
] );
if( arr.length > 0 ) localVar.buff.set( n-1,
arr );
var it = null;
var ite = ( localVar.list[0] )();
if( ite != null ) it = ite.snd;
localVar.list[1] = thi.pipeline( localVar.list[0], [ thi.takeWhile( isNotLF ), thi.map( function( item ) { return item.fst; } ) ] );
if( it == null ) {
list = undefined;
localVar.list = undefined;
return true;
}
return false;
};
//指定した行から1文字取り出す
this.getChar = function( idx ) {
if( !localVar ) return null;
var arr = localVar.buff.get( idx );
if( arr == null ) {
if( localVar.list && idx +
1 == n ) return ( localVar.list[1] )();
return null;
}
var it = null;
if( arr.length > 0 ) it = arr.shift();
if( arr.length == 0 ) {
localVar.buff.erase( idx );
if( !localVar.list && !localVar.buff.size()
) localVar = null;
}
return it;
};
this.isReleasable = function() { return ( !localVar ); };
function isNotLF( item ) { return ( item.fst !=
null && !( item.fst == '\r' && item.snd == '\n' ) ); }
//JavaScriptのMapに相当
function Map() {
var _arr = [];
function keyMatchIf( key, same, mismatch
) {
var item = thi.pipeline( thi.enumerate( 0 ), [ thi.zip( thi.convertIntoInfiniteList( _arr ) ), thi.dropWhile( function( it ) { return ( it.snd.key !== key ) } ), thi.head() ] );
return ( item == null ) ? ( function()
{ mismatch(); return null; } )() : same( item.fst );
}
this.set = function( key, val ) { return keyMatchIf( key, function( i ) { _arr[i].val = val; }, function() { _arr.push( { key:key, val:val } ); } ); };
this.get = function( key ) { return keyMatchIf(
key, function( i ) { return _arr[i].val; }, function() {} ); };
this.size = function() { return _arr.length;
};
//JavaScriptのdeleteに相当
this.erase = function( key ) { return keyMatchIf(
key, function( i ) { _arr.splice( i, 1 ); }, function() {} ); };
}
}
}
}
};
前バージョンからの主な変更点は
・InfiniteListオブジェクトの廃止
・pipeline関数の導入
です。
(2024.5.15)
c#で多重ループを抜けるためのヘルパークラス
厳格に履歴管理されているプロジェクトで、誰かが作った、ユニットテストコードのない、うんざりするほど長大なコードの多重ループから抜けるため
ヘルパークラスを作りました。(Visual Studio 2019で確認)
//-----------------------
// Form1.cs
//-----------------------
using System.Windows.Forms;
namespace WindowsFormsApp1
{
/// <summary>画面クラス</summary>
public partial class Form1 : Form
{
/// <summary>多重ループを抜けるためのヘルパークラス</summary>
private static class MultipleLoopEscapeHelper
{
/// <summary>状態</summary>
private enum State { Normal, Continue, Break };
private static State st = State.Normal;
private static uint cnt = 0;
/// <summary>ループに入る直前に初期化</summary>
public static void EntryBefore()
{
st = State.Normal;
cnt = 0;
}
/// <summary>状態をBreakにする</summary>
/// <param name="para_cnt">
/// para_cnt個上のループを抜ける</param>
public static void Break(uint para_cnt)
{
st = State.Break;
cnt = para_cnt - 1;
}
/// <summary>状態をContinueにする</summary>
/// <param name="para_cnt">
/// para_cnt個上のループをcontinue</param>
public static void Continue(uint para_cnt)
{
st = State.Continue;
cnt = para_cnt - 1;
}
/// <summary>ループ終了直後にContinueすべきときtrueを返す</summary>
public static bool IsEndAfter => st == State.Continue
|| st == State.Break;
/// <summary>ループ開始時にBreakすべきときtrueを返す</summary>
public static bool IsStart
{
get
{
if (st == State.Normal) return false;
if (st == State.Continue && cnt == 0)
{
EntryBefore();
return false;
}
if (st == State.Break && cnt == 0)
{
EntryBefore();
}
else
{
cnt--;
}
return true;
}
}
}
//画面の表示
public Form1()
{
InitializeComponent();
bool V = true;
MultipleLoopEscapeHelper.EntryBefore();
//LOOP1:
while (true)
{
if (MultipleLoopEscapeHelper.IsStart) break;
//誰かが書いた、うんざりするほど長大な処理
MultipleLoopEscapeHelper.EntryBefore();
//LOOP2:
while (true)
{
if (MultipleLoopEscapeHelper.IsStart) break;
//誰かが書いた、うんざりするほど長大な処理
MultipleLoopEscapeHelper.EntryBefore();
//LOOP3:
while (true)
{
if (MultipleLoopEscapeHelper.IsStart)
break;
//誰かが書いた、うんざりするほど長大な処理
switch (V)
{
case true:
V = false;
//3つ上のループをcontinueする
MultipleLoopEscapeHelper.Continue(3);//Java、JavaScriptの continue LOOP1; と同じ
continue;
case false:
//3つ上のループを抜ける
MultipleLoopEscapeHelper.Break(3);//Java、JavaScriptの
break LOOP1; と同じ。PHPの break 3; と同じ
continue;
default:
break;
}
//誰かが書いた、うんざりするほど長大な処理
}
if (MultipleLoopEscapeHelper.IsEndAfter)
continue;
//誰かが書いた、うんざりするほど長大な処理
}
if (MultipleLoopEscapeHelper.IsEndAfter) continue;
//誰かが書いた、うんざりするほど長大な処理
}
}
}
}
ヘルパークラスを作る利点として
1.goto文のように、ラベル名を考える必要がない
2.構造化プログラミング、オブジェクト指向プログラミングが常識の世の中で、例外的に、goto文を使わずに済む
3.多重ループ脱出用のフラグ名を考える必要がない
4.多重ループ脱出用のフラグが、メソッド内グローバル変数として振る舞うことを防止できる
参考文献: "break文",ウィキペディア フリー百科事典
(2020.04.15)
c#で多重ループを抜けるためのヘルパークラス(ラベル指定版)
厳格に履歴管理されているプロジェクトで、誰かが作った、ユニットテストコードのない、うんざりするほど長大なコードの多重ループから抜けるため
ヘルパークラスを作りました。(Visual Studio 2022 C#10.0で確認)
JavaやJavaScriptのようにループの抜け先をラベル指定できるものにしました。
//-----------------------
// Form1.cs
//-----------------------
namespace WinFormsApp1;
/// <summary>画面クラス</summary>
internal partial class Form1 : Form
{
/// <summary>多重ループを抜けるためのヘルパークラス</summary>
private static class MultipleLoopEscapeHelper
{
/// <summary>ラベル</summary>
internal enum Label { LOOP1, LOOP2, LOOP3 };
/// <summary>ラベルスタック</summary>
private static Stack<Label> labels = new Stack<Label>();
/// <summary>行き先のループのラベル</summary>
private static Label? gotoLabel;
/// <summary>状態</summary>
private enum State { Normal, Continue, Break };
private static State st = State.Normal;
/// <summary>ループに入る直前にラベルを付ける</summary>
/// <param name="label">
/// 開始するループ名</param>
internal static void EntryBefore(Label label)
{
if(labels.Contains(label))
{
//実行時エラーを発行する
throw new ArgumentOutOfRangeException(nameof(label),
"指定されたラベルは既に登録されています。");
}
labels.Push(label);
gotoLabel = null;
st = State.Normal;
}
/// <summary>行き先のループを抜ける</summary>
/// <param name="label">
/// 行き先</param>
internal static void Break(Label label)
{
gotoLabel = label;
st = State.Break;
}
/// <summary>行き先のループをContinueにする</summary>
/// <param name="label">
/// 行き先</param>
internal static void Continue(Label label)
{
gotoLabel = label;
st = State.Continue;
}
/// <summary>ループ終了直後にContinueすべきときtrueを返す</summary>
/// <param name="label">
/// 終了するループ名</param>
internal static bool IsEndAfter(Label label)
{
if (label == labels.Peek())
{
labels.Pop();
return st == State.Continue || st == State.Break;
}
//実行時エラーを発行する
throw new ArgumentOutOfRangeException(nameof(label),
"パラメーターのラベルは現在のループのラベルと違います。");
}
/// <summary>ループ開始時にBreakすべきときtrueを返す</summary>
internal static bool IsStart
{
get
{
if (st == State.Normal) return false;
if (gotoLabel != labels.Peek()) return true;
gotoLabel = null;
var isContinue = (st != State.Continue);
st = State.Normal;
return isContinue;
}
}
}
//画面の表示
internal Form1()
{
InitializeComponent();
var V = true;
System.Diagnostics.Trace.WriteLine("START");
//LOOP1:
MultipleLoopEscapeHelper.EntryBefore(MultipleLoopEscapeHelper.Label.LOOP1);
while (true)
{
System.Diagnostics.Trace.WriteLine("LOOP1.IsStart");
if (MultipleLoopEscapeHelper.IsStart) break;
//誰かが書いた、うんざりするほど長大な処理
//LOOP2:
MultipleLoopEscapeHelper.EntryBefore(MultipleLoopEscapeHelper.Label.LOOP2);
while (true)
{
System.Diagnostics.Trace.WriteLine("LOOP2.IsStart");
if (MultipleLoopEscapeHelper.IsStart) break;
//誰かが書いた、うんざりするほど長大な処理
//LOOP3:
MultipleLoopEscapeHelper.EntryBefore(MultipleLoopEscapeHelper.Label.LOOP3);
while (true)
{
System.Diagnostics.Trace.WriteLine("LOOP3.IsStart");
if (MultipleLoopEscapeHelper.IsStart) break;
//誰かが書いた、うんざりするほど長大な処理
switch (V)
{
case true:
V = false;
//LOOP1ループをcontinueする
System.Diagnostics.Trace.WriteLine(".Continue(LOOP1)");
MultipleLoopEscapeHelper.Continue(MultipleLoopEscapeHelper.Label.LOOP1);//Java、JavaScriptの
continue LOOP1; と同じ
continue;
case false:
//LOOP1ループを抜ける
System.Diagnostics.Trace.WriteLine(".Break(LOOP1)");
MultipleLoopEscapeHelper.Break(MultipleLoopEscapeHelper.Label.LOOP1);//Java、JavaScriptの
break LOOP1; と同じ
continue;
}
//誰かが書いた、うんざりするほど長大な処理
}
System.Diagnostics.Trace.WriteLine("LOOP3.IsEndAfter");
if (MultipleLoopEscapeHelper.IsEndAfter(MultipleLoopEscapeHelper.Label.LOOP3))
continue;
//誰かが書いた、うんざりするほど長大な処理
}
System.Diagnostics.Trace.WriteLine("LOOP2.IsEndAfter");
if (MultipleLoopEscapeHelper.IsEndAfter(MultipleLoopEscapeHelper.Label.LOOP2))
continue;
//誰かが書いた、うんざりするほど長大な処理
}
System.Diagnostics.Trace.WriteLine("END");
}
}
参考文献: 日本マイクロソフト株式会社 公式チャンネル,"BS3 # Visual Studio 2022 と .NET 6 での Windows アプリ開発技術の紹介",YouTube
(2022.07.16)
ローカル変数をグローバル変数化する技術
グローバル変数と、そのグローバル変数を変更するメソッドがある場合、そのメソッド前後でグローバル変数を評価すると、値が変化する。
また、参照型のローカル変数と、その変数を引数として取り、その参照先の値を変更するメソッドがある場合、そのメソッド前後で変数の参照先を評価すると、参照先の値が変化する。
このように、あるメソッドの前後で、値(または、参照先の値)が変わるローカル変数を「グローバル変数化したローカル変数」であると定義する。
厳格に履歴管理されていて、ユニットテストコードのないプロジェクトで、下記のようなクロージャーを使ったC#コードがある場合、Booメソッドの前後でlocalVariableを評価すると、値が変化するため、
localVariableは、グローバル変数化したローカル変数である。
参照型のローカル変数の場合、変更される値は参照先の値であるのに対し、クロージャーの場合は、ローカル変数の値が変更され、より悪質である。
(厳格に履歴管理されていて、ユニットテストコードのないプロジェクトで、下記のようなコードがあるような、三流プログラマが経験しやすい状況での話であり、クロージャーを全否定するものではありません。)
//メソッド開始
int localVariable = 0;//ローカル変数を定義
//誰かが書いた、うんざりするほど長大な処理
void Closure()//誰かが書いたクロージャ
{
//うんざりするほど長めの処理
localVariable += 1;//ローカル変数を変更
//うんざりするほど長めの処理
}
//誰かが書いた、うんざりするほど長大な処理
Boo(Closure);//誰かが書いた、クロージャーを実行する処理(実行前後で、localVariableの値が変わる)
(2020.06.01)
グローバル変数を置き換えるクラス
以下のように使われているグローバル変数A、Bを置き換えるクラスを作ってみました。(Visual Studio 2022 C#10.0で確認)
//-----------------------
// Form1.cs
//-----------------------
namespace WinFormsApp1;
public partial class Form1 : Form
{
/// <summary>グローバル変数A</summary>
private string A = "";
/// <summary>グローバル変数B</summary>
private int B;
public Form1()
{
InitializeComponent();
//メソッド開始
//Aに"文字列1"を設定する
A = "文字列1";
//Bに1を設定する
B = 1;
//誰かが書いた、うんざりするほど長大な処理
//サブメソッドの中身 開始
//誰かが書いた、うんざりするほど長大な処理
//サブ・サブ・・・サブメソッドの中
//誰かが書いた、うんざりするほど長大な処理
//Bに2を設定する
B = 2;
//ローカル変数名にAやBを使っている誰かが書いた多数のサブメソッドを呼び出す処理
//誰かが書いた、うんざりするほど長大な処理
//サブメソッドの中身 終了
//Aの値を取得する。Aをローカル変数に変更したいが、ここのAに"文字列1"が入っているかどうかは精査しないとわからない
_ = MessageBox.Show(A);
//Bの値を取得する。Bをローカル変数に変更すると2と出力すべきところ1が出力されてしまう。
_ = MessageBox.Show(Convert.ToString(B));
}
//AやBを更新しているがForm1()から呼び出されない誰かが書いた多数のメソッド
}
置き換え後のコードは以下になります。
//-----------------------
// Form1.cs
//-----------------------
namespace WinFormsApp1;
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
//メソッド開始
//グローバル変数AをGlobalVariable.Aクラスで置き換えた
var saveA = GlobalVariable.A.Value;
//GlobalVariable.Aに"文字列1"を設定する
saveA.SetValue_UniqueId1("文字列1");
//GlobalVariable.AのReaderを取得する
saveA.GetReader_UniqueId1(out GlobalVariable.A.IReader<string>?
readerA);
//グローバル変数BをGlobalVariable.Bクラスで置き換えた
var saveB = GlobalVariable.B.Value;
//GlobalVariable.Bに1を設定する
saveB.SetValue_UniqueId2(1);
//GlobalVariable.BのReaderを取得する(1回目)
saveB.GetReader_UniqueId2(out GlobalVariable.B.IReader<int>?
readerB1);
//誰かが書いた、うんざりするほど長大な処理
//サブメソッドの中身 開始
//誰かが書いた、うんざりするほど長大な処理
//サブ・サブ・・・サブメソッドの中
//誰かが書いた、うんざりするほど長大な処理
//GlobalVariable.Bに2を設定する
saveB.SetValue_UniqueId2(2);
//誰かが書いた、うんざりするほど長大な処理
//サブメソッドの中身 終了
//GlobalVariable.Aの値を取得する。readerA取得後、値を更新していないので実行時エラーにならない
var A = "";
readerA?.GetValue_UniqueId1(out A);
_ = MessageBox.Show(A);
//GlobalVariable.BのReaderを取得する(2回目)
saveB.GetReader_UniqueId2(out GlobalVariable.B.IReader<int>?
readerB2);
//GlobalVariable.Bの値を2回目に取得したReaderから取得する。readerB2取得後、値を更新していないので実行時エラーにならない
var B = 0;
readerB2?.GetValue_UniqueId2(out B);
_ = MessageBox.Show(Convert.ToString(B));
//GlobalVariable.Bの値を1回目に取得したReaderから取得する。readerB1取得後、値を更新しているのでデバッガーアタッチ時実行時エラーになる。デバッグなし実行時、実行時エラーにならないがログが出力される
readerB1?.GetValue_UniqueId2(out B);
_ = MessageBox.Show(Convert.ToString(B));
//ログメッセージをクリップボードに保存する
SimpleLog.Save();
}
/// <summary>グローバル変数を管理する静的クラス</summary>
private static class GlobalVariable
{
/// <summary>デバッガーアタッチ時実行時エラーを発行する</summary>
internal const bool IssueRuntimeError = true;
/// <summary>バージョン付き値クラス</summary>
private abstract class ValueWithVersion<T>
{
/// <summary>更新日時</summary>
protected DateTime _UpdateTime = DateTime.Now;
/// <summary>バージョン番号</summary>
protected ulong _VersionNumber;
/// <summary>値</summary>
protected T? _Value;
/// <summary>コンストラクタ</summary>
protected ValueWithVersion()
{
}
}
/// <summary>値を保持するクラス</summary>
private abstract class SaveValueBase<T> : ValueWithVersion<T>
{
/// <summary>値を読み出すオブジェクト</summary>
private ReaderBase<T>? _Reader;
/// <summary>値が更新された</summary>
private bool _UpdatedValue = true;
/// <summary>ログ</summary>
private readonly SimpleLog.CallingSide log = new();
/// <summary>コンストラクタ</summary>
protected SaveValueBase()
{
}
/// <summary>値を更新する</summary>
/// <param name="value">
/// 更新する値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <param name="callerMemberName">
/// 呼び出し元メソッド名</param>
protected void SetValue(T value, string callerFilePath,
int callerLineNumber, [System.Runtime.CompilerServices.CallerMemberName]
string callerMemberName = "")
{
//値を更新
_Value = value;
_UpdatedValue = true;
if (_UpdateTime == DateTime.Now)
{
//バージョン番号を更新
_VersionNumber++;
}
else
{
//更新日時を更新
_UpdateTime = DateTime.Now;
_VersionNumber = 0;
}
//呼び出し元をログに記録する
log.Add(callerFilePath, callerLineNumber, callerMemberName,
_UpdateTime, _VersionNumber);
}
/// <summary>値を読み出すオブジェクトを返す</summary>
/// <param name="retReader">
/// 値を読み出すオブジェクト(返却値)</param>
/// <param name="value">
/// 値を読み出すオブジェクトの新インスタンス</param>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
protected void GetReader(out ReaderBase<T>? retReader,
ReaderBase<T> value)
{
if (_UpdatedValue)
{
//値が更新された場合
//値を読み出すオブジェクトの新インスタンスをセットする
_Reader = value;
//値を読み出すオブジェクトの更新日時とバージョン番号を設定する
_Reader.Initialize(_UpdateTime, _VersionNumber);
_UpdatedValue = false;
}
//値を読み出すオブジェクトを返す
retReader = _Reader;
}
/// <summary>値を読み出す</summary>
/// <param name="retVal">
/// 返却値</param>
/// <param name="updateTime">
/// 更新日時</param>
/// <param name="versionNumber">
/// バージョン番号</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <param name="callerMemberName">
/// 呼び出し元メソッド名</param>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
internal void GetValue(out T? retVal, DateTime updateTime,
ulong versionNumber, string callerFilePath, int callerLineNumber, string
callerMemberName)
{
if (_UpdateTime != updateTime || _VersionNumber
!= versionNumber)
{
//更新日時やバージョン番号が呼び出し元と違う場合
//呼び出し元をログに記録する
log.Add(callerFilePath, callerLineNumber,
callerMemberName, updateTime, versionNumber);
//ログメッセージをSimpleLogへ送る
log.Save();
if (System.Diagnostics.Debugger.IsAttached
&& IssueRuntimeError)
{
//デバッガーアタッチ時
//ログメッセージをクリップボードに保存する
SimpleLog.Save();
//実行時エラーを発行する
throw new ArgumentOutOfRangeException(nameof(updateTime)
+ "," + nameof(versionNumber), "取得しようとしたバージョンの値は破棄されました。");
}
}
retVal = _Value;
}
}
/// <summary>値を読み出すクラス</summary>
private abstract class ReaderBase<T> : ValueWithVersion<SaveValueBase<T>>
{
/// <summary>コンストラクタ</summary>
/// <param name="value">
/// 値を保持するオブジェクト</param>
protected ReaderBase(SaveValueBase<T> value) =>
_Value = value;
/// <summary>更新日時とバージョン番号を設定する</summary>
/// <param name="updateTime">
/// 更新日時</param>
/// <param name="versionNumber">
/// バージョン番号</param>
internal void Initialize(DateTime updateTime, ulong versionNumber)
{
_UpdateTime = updateTime;
_VersionNumber = versionNumber;
}
/// <summary>値を読み出す</summary>
/// <param name="retVal">
/// 返却値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <param name="callerMemberName">
/// 呼び出し元メソッド名</param>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
protected void GetValue(out T? retVal, string callerFilePath,
int callerLineNumber, [System.Runtime.CompilerServices.CallerMemberName]
string callerMemberName = "")
{
if (_Value == null)
{
retVal = default;
return;
}
_Value.GetValue(out retVal, _UpdateTime, _VersionNumber,
callerFilePath, callerLineNumber, callerMemberName);
}
}
/// <summary>グローバル変数Aを代替するクラス</summary>
internal static class A
{
/// <summary>値を保持するオブジェクト</summary>
internal static readonly ISaveValue<string> Value
= new SaveValue<string>();
/// <summary>値を保持するインターフェース</summary>
/// <concept>C#10.0では制限できないがclass Aの外部で継承禁止</concept>
internal interface ISaveValue<T>
{
/// <summary>値を読み出すオブジェクトを返す</summary>
/// <param name="retReader">
/// 値を読み出すオブジェクト</param>
/// <concept>呼び出し箇所を明確にするためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
internal void GetReader_UniqueId1(out IReader<T>?
retReader);
/// <summary>値を更新する</summary>
/// <param name="value">
/// 更新する値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
internal void SetValue_UniqueId1(T value, [System.Runtime.CompilerServices.CallerFilePath]
string callerFilePath = "", [System.Runtime.CompilerServices.CallerLineNumber]
int callerLineNumber = 0);
}
/// <summary>値を保持するクラス</summary>
/// <concept>継承によるオーバーライド禁止</concept>
private sealed class SaveValue<T> : SaveValueBase<T>,
ISaveValue<T>
{
/// <summary>コンストラクタ</summary>
internal SaveValue() : base()
{
}
/// <summary>値を読み出すオブジェクトを返す</summary>
/// <param name="retReader">
/// 値を読み出すオブジェクト</param>
/// <concept>呼び出し箇所を明確にするためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void GetReader_UniqueId1(out IReader<T>?
retReader)
{
GetReader(out ReaderBase<T>? reader,
new Reader<T>(this));
retReader = reader as IReader<T>;
}
/// <summary>値を更新する</summary>
/// <param name="value">
/// 更新する値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
public void SetValue_UniqueId1(T value, [System.Runtime.CompilerServices.CallerFilePath]
string callerFilePath = "", [System.Runtime.CompilerServices.CallerLineNumber]
int callerLineNumber = 0)
{
SetValue(value, callerFilePath, callerLineNumber);
}
}
/// <summary>値を読み出すインターフェース</summary>
/// <concept>C#10.0では制限できないがclass Aの外部で継承禁止</concept>
internal interface IReader<T>
{
/// <summary>値を読み出す</summary>
/// <param name="retVal">
/// 読出し値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
internal void GetValue_UniqueId1(out T? retVal,
[System.Runtime.CompilerServices.CallerFilePath] string callerFilePath
= "", [System.Runtime.CompilerServices.CallerLineNumber] int
callerLineNumber = 0);
}
/// <summary>値を読み出すクラス</summary>
/// <concept>継承によるオーバーライド禁止</concept>
private sealed class Reader<T> : ReaderBase<T>,
IReader<T>
{
/// <summary>コンストラクタ</summary>
/// <param name="value">
/// 値を保持するオブジェクト</param>
internal Reader(SaveValueBase<T> value) :
base(value)
{
}
/// <summary>値を読み出す</summary>
/// <param name="retVal">
/// 読出し値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void GetValue_UniqueId1(out T? retVal, [System.Runtime.CompilerServices.CallerFilePath]
string callerFilePath = "", [System.Runtime.CompilerServices.CallerLineNumber]
int callerLineNumber = 0)
{
GetValue(out retVal, callerFilePath, callerLineNumber);
}
}
}
/// <summary>グローバル変数Bを代替するクラス</summary>
internal static class B
{
/// <summary>値を保持するオブジェクト</summary>
internal static readonly ISaveValue<int> Value
= new SaveValue<int>();
/// <summary>値を保持するインターフェース</summary>
/// <concept>C#10.0では制限できないがclass Bの外部で継承禁止</concept>
internal interface ISaveValue<T>
{
/// <summary>値を読み出すオブジェクトを返す</summary>
/// <param name="retReader">
/// 値を読み出すオブジェクト</param>
/// <concept>呼び出し箇所を明確にするためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
internal void GetReader_UniqueId2(out IReader<T>?
retReader);
/// <summary>値を更新する</summary>
/// <param name="value">
/// 更新する値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
internal void SetValue_UniqueId2(T value, [System.Runtime.CompilerServices.CallerFilePath]
string callerFilePath = "", [System.Runtime.CompilerServices.CallerLineNumber]
int callerLineNumber = 0);
}
/// <summary>値を保持するクラス</summary>
/// <concept>継承によるオーバーライド禁止</concept>
private sealed class SaveValue<T> : SaveValueBase<T>,
ISaveValue<T>
{
/// <summary>コンストラクタ</summary>
internal SaveValue() : base()
{
}
/// <summary>値を読み出すオブジェクトを返す</summary>
/// <param name="retReader">
/// 値を読み出すオブジェクト</param>
/// <concept>呼び出し箇所を明確にするためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void GetReader_UniqueId2(out IReader<T>?
retReader)
{
GetReader(out ReaderBase<T>? reader,
new Reader<T>(this));
retReader = reader as IReader<T>;
}
/// <summary>値を更新する</summary>
/// <param name="value">
/// 更新する値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
public void SetValue_UniqueId2(T value, [System.Runtime.CompilerServices.CallerFilePath]
string callerFilePath = "", [System.Runtime.CompilerServices.CallerLineNumber]
int callerLineNumber = 0)
{
SetValue(value, callerFilePath, callerLineNumber);
}
}
/// <summary>値を読み出すインターフェース</summary>
/// <concept>C#10.0では制限できないがclass Bの外部で継承禁止</concept>
internal interface IReader<T>
{
/// <summary>値を読み出す</summary>
/// <param name="retVal">
/// 読出し値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
internal void GetValue_UniqueId2(out T? retVal,
[System.Runtime.CompilerServices.CallerFilePath] string callerFilePath
= "", [System.Runtime.CompilerServices.CallerLineNumber] int
callerLineNumber = 0);
}
/// <summary>値を読み出すクラス</summary>
/// <concept>継承によるオーバーライド禁止</concept>
private sealed class Reader<T> : ReaderBase<T>,
IReader<T>
{
/// <summary>コンストラクタ</summary>
/// <param name="value">
/// 値を保持するオブジェクト</param>
internal Reader(SaveValueBase<T> value) :
base(value)
{
}
/// <summary>値を読み出す</summary>
/// <param name="retVal">
/// 読出し値</param>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <concept>ログにメソッド名を記録するためメソッド名をユニークにする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void GetValue_UniqueId2(out T? retVal, [System.Runtime.CompilerServices.CallerFilePath]
string callerFilePath = "", [System.Runtime.CompilerServices.CallerLineNumber]
int callerLineNumber = 0)
{
GetValue(out retVal, callerFilePath, callerLineNumber);
}
}
}
}
/// <summary>簡易ログクラス</summary>
internal static class SimpleLog
{
/// <summary>ログを出力する</summary>
private const bool _IsOutput = true;
/// <summary>ログメッセージ</summary>
private static string _Value = "";
/// <summary>ログメッセージを追加する</summary>
/// <param name="s">
/// ログメッセージ</param>
internal static void Add(string s)
{
if (_IsOutput) _Value += s + Environment.NewLine;
}
/// <summary>ログメッセージをクリップボードに保存する</summary>
internal static void Save()
{
if (_IsOutput) Clipboard.SetText(_Value);
_Value = "";
}
/// <summary>呼び出し側クラス</summary>
/// <concept>継承によるオーバーライド禁止</concept>
internal sealed class CallingSide
{
/// <summary>ログメッセージ</summary>
private string _Value = "";
/// <summary>ログメッセージを追加する</summary>
/// <param name="callerFilePath">
/// 呼び出し元ファイルパス名</param>
/// <param name="callerLineNumber">
/// 呼び出し元行数</param>
/// <param name="callerMemberName">
/// 呼び出し元メソッド名</param>
/// <param name="updateTime">
/// 更新日時</param>
/// <param name="versionNumber">
/// バージョン番号</param>
internal void Add(string callerFilePath, int callerLineNumber,
string callerMemberName, DateTime updateTime, ulong versionNumber)
{
if (_IsOutput) _Value += callerFilePath + "("
+ callerLineNumber + ")" + callerMemberName + "," +
updateTime.ToString("O") + "," + versionNumber.ToString()
+ Environment.NewLine;
}
/// <summary>ログメッセージをSimpleLogに保存する</summary>
internal void Save()
{
if (_IsOutput) SimpleLog.Add(_Value);
_Value = "";
}
}
}
}
参考文献: 日本マイクロソフト株式会社 公式チャンネル,"BS3 # Visual Studio 2022 と .NET 6 での Windows アプリ開発技術の紹介",YouTube
(2022.04.29)
DataSetをイミュータブルに管理する
C#でDataSetをイミュータブルに管理するラッパークラスを作りました。
以下のコードはVisual Studio 2019でコンパイル確認。コンセプトコードのためテストはしていません。
using System.Collections.Generic;
using System.Data;
using System.Windows.Forms;
namespace WindowsFormsApp1
{
/// <summary>画面クラス</summary>
public partial class Form1 : Form {
/// <summary>クロージャの代替インターフェース</summary>
/// <concept>クロージャを使わない。気軽に使わせない</concept>
private interface IClosureAlternative<T> {
void Run(T para_val);
}
/// <summary>DataSetをイミュータブルに管理するラッパークラス</summary>
/// <concept>継承によるオーバーライド禁止</concept>
private sealed class DataSetImmutable {
/// <summary>管理対象のDataSet(Dictionaryで管理)</summary>
private readonly Dictionary<string, DataTableImmutable> obj;
/// <summary>コンストラクタ</summary>
/// <param name="paraObj">
/// 格納するDataSet</param>
/// <concept>名前のないDataTableは管理対象外</concept>
public DataSetImmutable( DataSet paraObj ) {
obj = new Dictionary<string, DataTableImmutable>();
foreach (DataTable i in paraObj?.Tables) {
if (!string.IsNullOrEmpty(i?.TableName))
obj.Add(i.TableName, new DataTableImmutable( i ));
}
}
/// <summary>DataTable削除用コンストラクタ</summary>
/// <param name="paraObj">
/// 格納するDictionary</param>
/// <param name="paraTableNm">
/// 削除するDataTable名</param>
private DataSetImmutable( Dictionary<string, DataTableImmutable>
paraObj, string paraTableNm)
{
obj = new Dictionary<string, DataTableImmutable>(paraObj);
if (!string.IsNullOrEmpty(paraTableNm)) _ = obj.Remove(paraTableNm);
}
/// <summary>DataTable追加/更新用コンストラクタ</summary>
/// <concept>名前のないDataTableは管理対象外</concept>
/// <param name="paraObj">
/// 格納するDictionary</param>
/// <param name="paraDataTable">
/// 追加/更新するDataTable</param>
private DataSetImmutable( Dictionary<string, DataTableImmutable>
paraObj, string paraTableNm, DataTable paraDataTable ) : this( paraObj,
paraTableNm )
{
if (!string.IsNullOrEmpty(paraTableNm)) obj.Add(paraTableNm,
new DataTableImmutable( paraDataTable ) );
}
/// <summary>DataTableの追加/更新</summary>
/// <param name="retVal">
/// 生成したDataSetImmutable</param>
/// <param name="paraDataTable">
/// 追加/更新するDataTable</param>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void AddingOrUpdate(out DataSetImmutable retVal,
DataTable paraDataTable)
{
retVal = this;
if (paraDataTable != null) retVal = new DataSetImmutable(obj,
paraDataTable.TableName, paraDataTable);
}
/// <summary>DataTableの削除</summary>
/// <param name="retVal">
/// 生成したDataSetImmutable</param>
/// <param name="paraDataTableNm">
/// 削除するDataTable名</param>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void Deletion(out DataSetImmutable retVal, string
paraDataTableNm) => retVal = new DataSetImmutable(obj, paraDataTableNm);
/// <summary>管理対象のDictionaryをDataSetに変換しアクションに渡す</summary>
/// <param name="paraAct">
/// アクション</param>
/// <concept>クロージャを使わない。気軽に使わせない</concept>
/// <concept>内部の状態を無制限に提供しない、メッセージパッシング指向</concept>
public void GetDataSet(IClosureAlternative<DataSet>
paraAct)
{
if (paraAct == null) return;
DataSet dataSet = new DataSet();
foreach (KeyValuePair<string, DataTableImmutable>
i in obj)
{
i.Value.GetTable(dataSet);
}
paraAct.Run(dataSet);
}
/// <summary>DataTable名のDataTableをDataSetに変換しアクションに渡す</summary>
/// <param name="paraAct">
/// アクション</param>
/// <param name="paraTableNm">
/// DataTable名</param>
/// <concept>クロージャを使わない。気軽に使わせない</concept>
/// <concept>内部の状態を無制限に提供しない、メッセージパッシング指向</concept>
public void GetDataTable(IClosureAlternative<DataSet>
paraAct, string paraTableNm)
{
if (paraTableNm == null || paraAct == null) return;
if ( !obj.TryGetValue( paraTableNm, out DataTableImmutable
dti ) ) return;
DataSet dataSet = new DataSet();
dti.GetTable(dataSet);
paraAct.Run(dataSet);
}
/// <summary>DataTableをイミュータブルに管理するラッパークラス</summary>
private sealed class DataTableImmutable
{
/// <summary>管理対象のDataTable</summary>
private readonly DataTable obj;
/// <summary>コンストラクタ</summary>
/// <param name="paraObj">
/// 格納するDataTable</param>
public DataTableImmutable( DataTable paraObj )
{
//格納するDataTableをコピーして管理対象にする
obj = paraObj?.Copy();
DisableReferenceType();
}
/// <summary>string型以外の参照型フィールドの参照を削除する</summary>
private void DisableReferenceType()
{
for (int i = 0; i < (obj?.Columns.Count
?? 0); i++)
{
switch (obj.Columns[i].DataType.ToString())
{
case "System.Boolean":
case "System.Byte":
case "System.Char":
case "System.DateTime":
case "System.Decimal":
case "System.Double":
case "System.Int16":
case "System.Int32":
case "System.Int64":
case "System.SByte":
case "System.Single":
case "System.String":
case "System.TimeSpan":
case "System.UInt16":
case "System.UInt32":
case "System.UInt64":
break;
default://string型以外の参照型フィールドの場合
string columnName = obj.Columns[i].ColumnName;//フィールドを削除する前にフィールド名を保存する
//フィールドを削除
obj.Columns.Remove(obj.Columns[i]);
//削除した場所に空のフィールド追加する
obj.Columns.Add(columnName, typeof(string)).SetOrdinal(i);
break;
}
}
}
/// <summary>管理対象のDataTableを出力用DataSetにコピーする</summary>
/// <param name="paraForOutput">
/// 出力用DataSet</param>
/// <concept>内部の状態を無制限に提供しない、メッセージパッシング指向</concept>
public void GetTable(in DataSet paraForOutput)
=> paraForOutput.Tables.Add(obj?.Copy());
}
}
//画面の表示
public Form1()
=> InitializeComponent();
}
}
(2020.06.14)
自動コミット機能付きList
C#で作りました。
読み取りをするまでは、自由に変更でき、読み取り後はイミュータブルになります。
以下のコードはVisual Studio 2019でコンパイル確認。コンセプトコードのためテストはしていません。
using System.Collections.Generic;
using System.Windows.Forms;
namespace WindowsFormsApp1
{
/// <summary>画面クラス</summary>
public partial class Form1 : Form {
/// <summary>自動コミット機能付きリスト</summary>
/// <concept>継承によるオーバーライド禁止</concept>
private sealed class ListWithAutoCommitFeature<T> //
Tに、string型以外の参照型を使うと、コミット後も変更できてしまうので注意
{
/// <summary>管理対象のリスト</summary>
private readonly List<T> _list = new List<T>();
/// <summary>コミット済みフラグ</summary>
private bool _committedFlag = false;
/// <summary>コンストラクタ</summary>
public ListWithAutoCommitFeature() {
}
/// <summary>データの取得</summary>
/// <param name="retVal">
/// 取得データ</param>
/// <param name="paraIdx">
/// 取得するデータのインデックス</param>
/// <concept>1回でも読み出されたらコミットする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void GetValue(out T retVal, int paraIdx)
{
_committedFlag = true;//コミットする
retVal = _list[paraIdx];
}
/// <summary>管理対象のListをコピーして返す</summary>
/// <param name="retTs">
/// 出力List</param>
/// <concept>1回でも読み出されたらコミットする</concept>
/// <concept>ローカル変数を使用させるため、参照渡しで返す</concept>
public void GetList( out List<T> retTs )
{
_committedFlag = true;//コミットする
retTs = new List<T>( _list );
}
/// <summary>データの追加</summary>
/// <param name="paraVal">
/// 追加するデータ</param>
/// <param name="paraErr">
/// true:コミット後はエラーにする</param>
/// <concept>コミット後は変更できない</concept>
public void Add( T paraVal, bool paraErr = true )
{
if (!ErrorHandingAfterCommit(paraErr)) _list.Add(paraVal);
}
/// <summary>データの更新</summary>
/// <param name="paraIdx">
/// 更新するデータのインデックス</param>
/// <param name="paraVal">
/// 更新データ</param>
/// <param name="paraErr">
/// true:コミット後はエラーにする</param>
/// <concept>コミット後は変更できない</concept>
public void SetItem( int paraIdx, T paraVal, bool paraErr = true )
{
if (!ErrorHandingAfterCommit(paraErr)) _list[paraIdx]
= paraVal;
}
/// <summary>データの削除</summary>
/// <param name="paraIdx">
/// 削除するデータのインデックス</param>
/// <param name="paraErr">
/// true:コミット後はエラーにする</param>
/// <concept>コミット後は変更できない</concept>
public void RemoveAt(int paraIdx, bool paraErr = true)
{
if (!ErrorHandingAfterCommit(paraErr)) _list.RemoveAt(paraIdx);
}
/// <summary>コミット後エラー処理</summary>
/// <param name="paraErr">
/// true:コミット後はエラーにする</param>
/// <returns>コミット後ならtrue</returns>
private bool ErrorHandingAfterCommit( bool paraErr )
{
if (!_committedFlag) return _committedFlag;
if (paraErr) _ = _list[_list.Count];//実行時エラーにする
return _committedFlag;
}
}
//画面の表示
public Form1()
=> InitializeComponent();
}
}
参考文献:時計屋, "Immutableなモノたち", Qiita
(2020.06.20)
Maximaで卵形線であることを確認する
平面曲線の曲率を以下のように定義する。
curvature( t, x, y ) := ( diff( x, t ) * diff( y, t, 2 ) - diff( x, t, 2 ) * diff( y, t ) )
/ ( diff( x, t )^2 + diff( y, t )^2 )^(3/2)$
パラメータの意味は、curvature( t = 媒介変数, x = 曲線のx座標, y = 曲線のy座標 );
曲線の回転数を以下で定義する。
rotation_number( t, x, y, a, b ) := float( romberg( trigreduce( curvature( t, x, y ) * sqrt( diff( x, t )^2
+ diff( y, t )^2 ) ), t, a, b )/(2*%pi) )$
パラメータの意味は、
rotation_number( t = 媒介変数, x = 曲線のx座標, y = 曲線のy座標, a = 媒介変数の始点, b = 媒介変数の終点 );
結果は数値積分による近似値が返されるが、a と b での座標が一致し滑らかであれば理論値は整数となるため多少の誤差は気にしない気にしない。
以下の例では回転数が1に近ければよい。
曲率のグラフは以下で表示する。( 表示範囲が -2π≦t≦2πの場合)
plot2d(curvature( t, x(t), y(t)), [t,-2*%pi,2*%pi]);
以下の例では曲率 > 0 、
0≦t<2πの範囲で極値が4個以上確認できればよい。
参考文献:小林昭七, "曲線と曲面の微分幾何", 裳華房
赤間世紀, "Maximaで学ぶコンピュータ代数", 工学社
梅原雅顕, 山田光太郎, "曲線と曲面 - 微分幾何学的アプローチ", 裳華房
(2010.12.30)
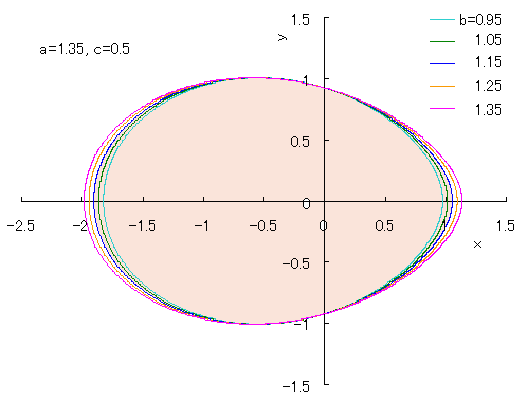
卵形曲線(回転する円の半径と中心を振動させる)
x 軸上に4点 E, F, G, H ( EF = a, FG = b, GH = c )がこの順番で並んでいるとき
x = b cosθ/ 2 + r (θ) cosθ
y = r (θ) sinθ
r (θ) = { a + c + (c - a) cosθ} / 2
最大直径は a + b + c
推奨値 a = 1.35, b = 1.15, c = 0.5
a = c のとき、楕円
さらに、b = 0 のとき、円になる。
(2009.08.22)

この画像は茨城県ひたちなか市の山本信雄 氏のご厚意により、ご提供頂いたものです。
(2009.09.27)
a, b, c に推奨値を代入しMaxima に入力するには以下のようにする。
r(t):=(1.35+0.5+(0.5-1.35)*cos(t))/2;
x(t):=1.15*cos(t)/2+r(t)*cos(t);
y(t):=r(t)*sin(t);
回転数と曲率のグラフは以下で確認する。
rotation_number( t, x(t), y(t), 0, 2*%pi);
plot2d(curvature( t, x(t), y(t)), [t,-2*%pi,2*%pi]);
(2010.12.30)
上式は
g ( x ) = [ √{ 8(c-a)x + (a+b+c)2 } - (a+b+c) ] / (2c-2a)
y2 = { a + c + (c - a) g (x) }2 (1 - g (x)2 ) / 4
と変形できるので「雌鶏変換」の特別な場合でした。
(2012.01.15)
卵形曲線(ヘビサイド関数を使用する蛇道な方法)
[ ( x - c ) / { c + 2( a - c ) u( x - c ) } ]2 + ( y / b )2 = 1
u(x) = ( sgn(x) + 1 ) / 2
0 < c < 2a
c = a のとき楕円
(2009.09.20)
a = 1, b = 0.72, c = 0.9
この画像は茨城県ひたちなか市の山本信雄 氏のご厚意により、ご提供頂いたものです。
(2009.12.20)
参考文献:イアン・スチュアート, "数学の魔法の宝箱", ソフトバンククリエイティブ
(2010.08.15)
上式は
y2 = b2 - [ b ( x - c ) / { c + 2( a - c ) u( x - c ) } ]2
と変形できるので「雌鶏変換」の特別な場合でした。
(2012.01.15)
野球ボールの表面の曲線
r をボールの半径
d を |d| < r とすると
f ( t ) = √[ { 2 t ( r2 - d2 ) / ( 2 d ) + r2 - t2 } / 2 ]
P( d cos( s ), f( d cos( s ) ), f( - d cos( s ) ) )
Q( d cos( s ), f( d cos( s ) ), - f( - d cos( s ) ) )
R( d cos( s ), - f( d cos( s ) ), f( - d cos( s ) ) )
S( d cos( s ), - f( d cos( s ) ), - f( - d cos( s ) ) )
をつないだ曲線で表すことができる。
(2011.11.12)
(2011.12.11)訂正
野球ボールの表面の曲線
f ( x ) = { ( ea + 1 ) ea x - ea - 1 } / { ( ea - 1 ) ea x + ea - 1 }
φ( x ) = ( π- 2 d ) ( f( cos( 2 x ) ) + 1 ) / 2 + d
野球ボールの表面の曲線は
x(θ) = r sin( φ(θ) ) cos(θ)
y(θ) = r sin( φ(θ) ) sin(θ)
z(θ) = r cos( φ(θ) )
で表すことができる。
推奨値:r = 3.5, a = 3.5, d = 0.5
(2011.11.12)
野球ボールの表面の曲線
上式で
f ( x ) = Atan( a x ) / Atan( a )
としてもよい。
推奨値:r = 3.5, a = 0.9, d = 0.6
(2011.11.20)
楕円と、フーリエ級数を使わない三角波、ノコギリ波
a を定数として
y = ±a sin( Acos( x ) )
y = ±a cos( Asin( x ) )
は、それぞれ楕円となる。
y = Asin( sin( x ) )
y = Asin( cos( x ) )
y = Acos( sin( x ) )
y = Acos( cos( x ) )
は、それぞれ三角波となる。
y = Atan( tan( x ) )
は、ノコギリ波となる。
階段関数
f ( x ) = Atan( tan( - x ) ) + x
とすると
[ x ] = f ( π ( x - 1/2 ) ) / π
となる。
卵割線
卵曲面が卵曲線
z = x(φ)
y = y(φ)
0≦φ≦π
を(z軸を軸に)1回転して定義されているとする。
0<a<π、0<b<π、a ≠ b
φ(θ) = ( b - a ) Acos( cos( n θ) ) / π + a
とすると卵曲面上の卵割線は
x = y(φ(θ)) cosθ
y = y(φ(θ)) sinθ
z = x(φ(θ))
となる。
(2011.12.10)
整数と円周率は仲がいい
整数論の公式に円周率が現れると、神秘的だと、よく言われるが
整数とは実数空間上に周期的に現れる数のことだから
それほどでもない。
(2011.12.18)
螺旋階段
f(x)= Atan( tan( - x ) ) + x
P( s cos t, s sin t, f (π (t - 1/2 ) ) / π)
0≦s≦a
(2012.12.08)
任意の三角波
-π/2 < a < π/2 のとき
f ( x ) = (|x| + x) / 2
g ( x ) = Atan( tan x )
とおくと任意の三角波は
y = { 4π f ( g (x) - a ) - 2 ( g (x) - a ) ( π - 2a ) } / ( π2 - 4a2 )
となる。
(2012.01.01)
任意の三角波
上式で
y = 2 f ( g (x) - a ) / (π-2a) + 2 f ( a - g (x) ) / (π+2a)
としてもよい。
(2012.01.03)
無限クローン波
y = f ( Atan( tan( x ) ) )
合わせ鏡波
y = f ( Acos( cos( x ) ) )
正多角形(正n角形)
f ( x ) = Acos( cos(nx) ) / n
r (θ) = a / cos( f (θ) - π / n )
n 稜星
f ( x ) = Acos( cos(nx) ) / n
r (θ) = a / cos( f (θ) + π / n )
激変星
f ( x ) = Acos( cos(nx) ) / n
r (θ) = a / cos( f (θ) + t )
n を整数として t を動かす。
(2011.12.30)
n 芒星(nが奇数の場合)
f (θ) = 2 Acos( cos( n θ / 2 ) ) / n
r (θ) = a / cos( f (θ) - 4π )
n = 5 のとき五芒星
n が偶数の場合は正n/2角形
(2012.01.07)
太極図
f (x) = ( x + |x| ) / 2
g ( x, y ) = f ( x + y ) - f ( x - y ) - y
h ( x, y ) = √( y2 - g ( x, y )2)
p ( x, y ) = 6 Asin( cos( y x ) ) / ( yπ)
q (x) = h ( x + 2, 1 ) - h ( x + 1/2, 1/2 ) + h ( x - 1/2, 1/2 ) - h ( x - 2, 1 )
とすると、太極図のパラメータ表示は
x (θ) = p (θ, 3 )
y (θ) = q ( - p (θ, 1 ) )
となる。
階段関数を連続関数で近似する
a < 1 で 1 に十分近いとすると
f (x) = ( x + |x| ) / 2
g (x) = Atan( tan(π( x - 1 / 2 ) ) ) /π+ 1 / 2
h (x) = f ( x - a ) / ( 1 - a ) + f ( a - x ) / a
y = a h ( g (x) ) + x - a
(2012.03.24)
ヒストグラム
区間幅をh、区間数をn
区間 a ~ a + h の値をy1
区間 a + h ~ a + 2 h の値をy2
…
区間 a + (n-1) h ~ a + n h の値をyn
とするときのヒストグラムは
f (x) = ( sign(x) + 1 ) / 2
g (x) = f (x) - f ( x - 1 )
y (x) = Σ{ k = 1~n } yk g ( ( x - ( a + ( k - 1 ) h ) ) / h ) + y0 f ( - x + a ) + y0 f ( x - ( a + n h ) )
y0は通常0(y が確率値で区間外をベースレートにしたいときに使用する)
境界の値は、ご愛嬌
(2016.11.06)
単位ステップ関数
u (t) = ( - sign2 (t) + sign (t) + 2 ) / 2
(2016.11.12)
四分位点を通る折れ線グラフ
a, b, c, d, m を 0%点 、25%点 、50%点 、75%点 、100%点の x 座標とすると
この5点を通る折れ線グラフは
f (x) =g ( (x - a) / (b - a) ) + g ( (x - b) / (c - b) ) + g ( (x - c) / (d - c) ) + g ( (x - d) / (m - d) )
g (x) = 0.25 { h (x) - h (x - 1) }
h (x) = ( x + |x| ) / 2
となる。
平行四辺形と撞球軌道
x = a Acos( cos( b t + c ) )
y = d Acos( cos( p t + q ) )
は撞球軌道となり、特別な場合に平行四辺形となる。
角楕円長方形
a ≧ 0, b, c≧ 0, d が定数の時
( g ( x, a ) / b )^2 + ( g ( y, c ) / d )^2 = 1
g ( x, y ) = h ( x - y ) - h ( - x - y )
h (x) = ( x + |x| ) / 2
は角楕円長方形となる
(2012.03.18)
2n+1本三つ編み
xk(t) = cos( t + 2kπ/(2n+1) )
yk(t) = sin( 2 ( t + 2kπ/(2n+1) ) )
zk(t) = a t
(k = 0,1,…,2n)
ルーローの三角形
f (θ) = 2 Acos( cos( 3 θ/ 2 ) ) / 3
r (θ) = √( 11sin2 f(θ) + 2 √(3) cos f(θ) sin f(θ) + 9cos2 f(θ) ) - √(3) sin f(θ) - cos f(θ)
(2012.01.08)
全波整流波、半波整流波
f ( x ) = sin ( Acos ( cos x ) )
で全波整流波となる。
g ( x ) = ( x + |x| ) / 2
f ( x ) = g ( sin x )
で半波整流波となる。
(2012.01.21)
つながった太極図
g ( x ) = ( x + |x| ) / 2
h ( x ) = g ( 2Asin( sin(πx/2) ) / π )
f ( x ) = √( 1- ( h(x) - 1 )2 ) - √( 1 - ( h(x-2) - 1 )2 )
次の3式を同一座標上に重ねて書くと
y1 = f ( x )
y2 = 2 f ( x / 2 )
y3 = - 2 f ( x / 2 )
一直線に並んだ太極図になる。
(2012.01.22)
双子葉
r (θ) = Atan( tanθ)
爪車
n を整数として
r (θ) = a Atan( tan ( nθ+ b t ) ) + s
(2011.12.31)
(n-1)穴トーラス
z2 = - T2n(x) - 8 y2 (y2 - 1)
ただし、n≧2
Tm(x):第一種チェビシェフ多項式
(2012.10.18)
(n+1)穴トーラス
f (x,y) = √[ ( x2 - 1 ) { cos( n y ) - a - x2 } ]
P( { t cos( u + s/2 ) - f (t,s) sin( u + s/2 ) + 1.5 } cos s, { t cos(u+s/2) - f (t,s) sin( u + s/2 ) + 1.5 } sin s, t sin( u + s/2 ) + f (t,s) cos( u + s/2 ) )
-1≦ t ≦1
0 < a < 1
花1(桜の花)
r (θ) = Acos( cos( Acos( cos( nθ) ) - a ) )
n = 5
π<a<2π
の時、桜の花
花2
r (θ) = |cos(nθ/2)|+a
花3
r (θ) = √(1-(f ( nθ)2) + a
f (x) = 2 Asin( sin(x/2) ) /π
16進デジタル数字
f(x)=(|x|-|x-1|+1)/2
0:
x(t)=1-f(t)+f(t-3)
y(t)=1-f(t-1)-f(t-2)+f(t-4)+f(t-5)
1:
x(t)=1
y(t)=1-f(t)-f(t-1)
2:
x(t)=f(t)-f(t-2)+f(t-4)
y(t)=1-f(t-1)-f(t-3)
3:
x(t)=f(t)-f(t-2)+f(t-3)-f(t-5)
y(t)=1-f(t-1)-f(t-4)
4:
x(t) = f(t-1)
y(t)=1-f(t)+f(t-2)-f(t-3)-f(t-4)
5:
x(t)=1-f(t)+f(t-2)-f(t-4)
y(t)=1-f(t-1)-f(t-3)
6:
x(t)=1-f(t)+f(t-3)-f(t-5)
y(t)=1-f(t-1)-f(t-2)+f(t-4)
7:
x(t)=f(t-1)
y(t)=f(t)-f(t-2)-f(t-3)
8:
x(t)=1-f(t)+f(t-2)-f(t-4)+f(t-6)
y(t)=1-f(t-1)-f(t-3)+f(t-5)+f(t-7)
9:
x(t)=1-f(t-1)+f(t-3)-f(t-5)
y(t)=f(t)-f(t-2)-f(t-4)
A:
x(t)=1-f(t)+f(t-4)
y(t)=1-f(t-1)-f(t-2)+f(t-3)-f(t-5)+f(t-6)+f(t-7)
b:
x(t)=f(t-2)-f(t-4)
y(t)=1-f(t)-f(t-1)+f(t-3)
C:
x(t)=1-f(t)+f(t-3)
y(t)=1-f(t-1)-f(t-2)
d:
x(t)=1-f(t)+f(t-2)
y(t)=-f(t-1)+f(t-3)+f(t-4)
E:
x(t)=1-f(t)+f(t-2)-f(t-3)+f(t-5)
y(t)=1-f(t-1)-f(t-4)
F:
x(t)=1-f(t)+f(t-2)-f(t-3)
y(t)=1-f(t-1)-f(t-4)
(2012.09.23)
曲(卵形)面上の螺旋
曲面が
x = x ( θ )
y = y ( θ )
0≦θ≦π
で表示される曲線を x 軸を軸に1回転させて定義されているとき
その面上の螺旋は a を定数(推奨2以上)として
x = x ( θ )
y = y ( θ ) sin( a θ)
z = y ( θ ) cos( a θ)
0≦θ≦π
で表現できる。
参考文献:
Spherical Spiral
http://mathworld.wolfram.com/SphericalSpiral.html
早苗雅史、球面螺旋
http://izumi-math.jp/sanae/MathCurves/MathCurves.htm
(2011.01.09)
xi = x ( θ )
yi = y ( θ ) sin( a θ + αi )
zi = y ( θ ) cos( a θ + αi )
0≦θ≦π
0≦α1<α2<α3<…<αn<2π
とすれば n 重螺旋となる。
(2011.01.15)
曲線が弧長パラメータ t を用いて
x = x ( t )
y = y ( t )
0≦t≦L
と表示されているとする。
この曲線を x 軸を軸に1回転させて定義される曲面上の
等幅螺旋(皮むき線)は a、α を定数(0<|a|≦1/2を推奨)として
x = x ( t )
y = y ( t ) sin( 2 π t / ( a L ) + α )
z = y ( t ) cos( 2 π t / ( a L ) + α )
0≦t≦L
と表現できる。
(2011.01.29)
卵形曲線(楕円を y 軸方向へ非一様に拡大する)
( x / a )2 + [ b y / { 1 + ( x + a ) / c } ]2 = 1
推奨値 a = 1.5, b = 1.2, c = 8
(2009.08.22)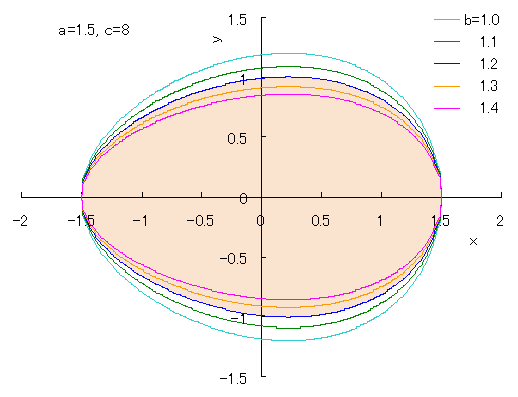
この画像は茨城県ひたちなか市の山本信雄 氏のご厚意により、ご提供頂いたものです。
(2009.09.27)
上式を極座標表示に変換すると
x = a cosθ
y = { 1 + ( a + a cosθ) / c } sinθ/ b
a, b, c に推奨値を代入しMaxima に入力するには以下のようにする。
x(t):=1.5*cos(t);
y(t):=(1+1.5*(1+cos(t))/8)*sin(t)/1.2;
回転数と曲率のグラフは以下で確認する。
rotation_number( t, x(t), y(t), 0, 2*%pi);
plot2d(curvature( t, x(t), y(t)), [t,-2*%pi,2*%pi]);
参考文献:山本信雄, "卵形曲線の方程式(その5)", TDCC研究室支局
(2010.12.30)
一般化
( x / a )2 + { y / ( b x + c ) }2 = 1
b = 1 / ( b ' c ' ) , c = ( 1 + a / c ' ) / b ' とおくと上式に一致する。
b = c ' / a , c = b ' とおくと茨城県ひたちなか市の山本信雄 氏 提案の(3)式に一致する。
(2009.12.20)
参考文献:cubic egg
http://www.2dcurves.com/cubic/cubiceg.html
(2011.05.05)
上式は「雌鶏変換」の特別な場合でした。
(2011.06.25)
卵形曲線(一次式と二次式の差を利用する方法)
( a x2 + b x + c )2 / ( d x + e )2 + ( y / f )2 = 1
推奨式は
( ( x - 1.35 ) ( g x + 1 ) )2 / ( 1.35 ( 1.3 x + 1) )2 + ( y / 1.1 )2 = 1
g の推奨値は 1
ただし、x ≧0
x <0 の領域に余分な図形が出現しますが
g = 0.6 とすると、おむすびと卵のランチセットになります。
(2011.05.08)
上式は「雌鶏変換」の特別な場合でした。
(2011.06.25)
卵形曲線(円を x 軸のプラス方向に徐々に引き伸ばす)
x = { (c - 2) cosθ+ c + 2} r (cosθ+ 1) / 4
y = r sinθ
最大直径は c r
c < 1 のとき、三日月状曲線
1 ≦ c < 2 のとき、うちわ形曲線
c = 2 のとき、円
2 < c のとき、卵形曲線
(2009.07.26)
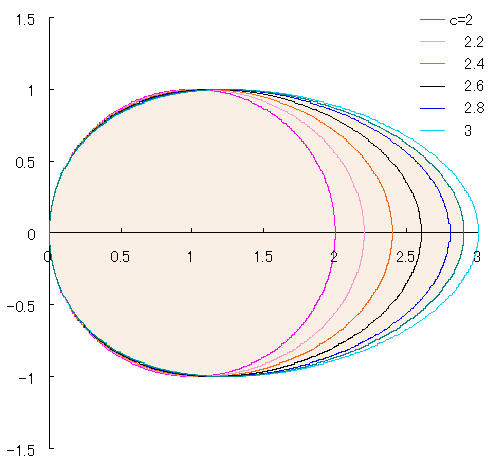
この画像は茨城県ひたちなか市の山本信雄 氏のご厚意により、ご提供頂いたものです。
卵形曲線の導出方法について
上記の卵形曲線は中心点(r, 0)、半径 r の円を x 軸のプラス方向に徐々に引き伸ばすことにより導出しました。
(2009.08.08)
r = 1, c = 3 としMaxima に入力するには以下のようにする。
x(t):=((3-2)*cos(t)+3+2)*(cos(t)+1)/4;
y(t):=sin(t);
回転数と曲率のグラフは以下で確認する。
rotation_number( t, x(t), y(t), 0, 2*%pi);
plot2d(curvature( t, x(t), y(t)), [t,-2*%pi,2*%pi]);
(2010.12.30)
上の卵形曲線式を一般化した
x = a ( 1 + cosθ) ( b + cosθ)
y = c sinθ
推奨値:a = 1/6、b = 8、c = 1.1
という式を思いつきましたが
上の卵形曲線式は Massimo Vaglieco 氏提案の
x = a cos t + c cos 2t
y = b sin t
http://www.mathcurve.com/courbes2d/oeuf/oeufgranville.shtml
の特別な場合でした。
(2011.5.7)
上式は「雌鶏変換」の特別な場合でした。
(2011.06.25)
スライダー(ピストン)クランク機構が描く卵形曲線
原点を中心に回転する棒Aの長さを r
棒A とスライダをつなぐ棒Bの長さを L
棒B上の任意の点Cとスライダまでの長さを z
とするとき、点Cの軌跡は卵形になっている。
x = r cosθ + ( 1 - t ) √( L2 - r2 sin2θ)
y = t r sinθ
ただし、t = z / L
推奨値 r = 1.5, L = 2.25, t = 11/15
参考文献:横田博史, "はじめてのMaxima", 工学社
太田安彦、ピストン・クランク機構の力学 http://www.geocities.jp/bequemereise/piston-crank.html
(2010.09.12)
r, L, t に推奨値を代入しMaxima に入力するには以下のようにする。
x(t):=1.5*cos(t)+(1-11/15)*sqrt(2.25^2 - 1.5^2 * sin(t)^2);
y(t):=11*1.5*sin(t)/15;
回転数と曲率のグラフは以下で確認する。
rotation_number( t, x(t), y(t), 0, 2*%pi);
plot2d(curvature( t, x(t), y(t)), [t,-2*%pi,2*%pi]);
(2010.12.30)
上式は「雌鶏変換」の特別な場合でした。
(2011.06.25)
スライダー(ピストン)クランク機構
r , Lは上式と同じとする。
f (x) = ( |x| - |x-1| + 1 ) / 2
x (θ,t) = r f ( t ) cosθ + f ( t - 1 ) √( L2 - r2 sin2θ )
y (θ,t) = r f ( t ) sinθ- r f ( t - 1 ) sinθ
チェビシェフリンク
f (x) = ( |x| - |x-1| + 1 ) / 2
g ( x ) = √( ( 5 + cos x ) / ( 5 - 4 cos x ) )
x (θ,t) = ( 2 + cos θ) / 2 + g (θ) sinθ + ( ( 2 - cosθ) / 2 - g (θ) sinθ)
f ( t ) - 2 f ( t - 1 ) + f ( t - 2 ) cosθ+ ( 2 + 2 g (θ) sinθ - cosθ)
f ( t - 3 )
y (θ,t) = sinθ/ 2 + ( 2 - cosθ) g (θ) - ( sinθ/ 2 + ( 2 - cosθ) g (θ) )
f ( t ) + f ( t - 2 ) sinθ+ ( 2 ( 2 - cosθ) g (θ) - sinθ) f ( t - 3 )
参考文献:Hyrodium, "Tchebicheff Link", Hyrodium laboratory
n 角形
n 角形の頂点の座標を ( x0 , y0 ) , ( x1 , y1 ) , … , ( xn , yn ) とする。ただし、xn = x0, yn = y0
f (x) = ( |x| - |x-1| + 1 ) / 2
x ( t ) = x0 + Σ{ k=0 ~ n-1 } ( x k+1 - x k ) f ( t - k )
y ( t ) = y0 + Σ{ k=0 ~ n-1 } ( y k+1 - y k ) f ( t - k )
時計
h時m分とする。
f (x) = ( |x| - |x-1| + 1 ) / 2
長針:
x ( t ) = f ( t ) sin ( 2 π ( 60 h + m ) / 60 )
y ( t ) = f ( t ) cos ( 2 π ( 60 h + m ) / 60 )
短針:
x ( t ) = f ( t ) sin ( 2 π ( 60 h + m ) / 720 )
y ( t ) = f ( t ) cos ( 2 π ( 60 h + m ) / 720 )
(2014.07.27)
テオ・ヤンセン機構
f ( x , y , z , w ) = ( x2 + y2 + z2 - w2 ) / 2
g ( x , y , z , w ) = ( x f ( x , y , z , w ) + y √( ( x2 + y2 ) z2 - f ( x , y , z , w )2 ) ) / ( x2 + y2 )
h ( x ) = ( |x| - |x - 1| + 1 ) / 2
f0 ( x ) = g ( -38 + 15 cos ( x ) , 7.8 + 15 sin ( x ) , 41.5 , 50 )
f1 ( x ) = g ( 7.8 + 15 sin ( x ) , 38 - 15 cos ( x ) , 41.5 , 50 )
f2 ( x ) = g ( -38 + 15 cos ( x ) , -7.8 - 15 sin ( x ) , 39.3 , 61.9 )
f3 ( x ) = g ( 7.8 + 15 sin ( x ) , -38 + 15 cos ( x ) , 39.3 , 61.9 )
f4 ( x ) = g ( h ( x ) , f1 ( x ) , 40.1 , 55.8 )
f5 ( x ) = g ( f1 ( x ) , -h ( x ) , 40.1 , 55.8 )
f6 ( x ) = f2 ( x ) + g ( f4 ( x ) - f2 ( x ) , f5 ( x ) - f3 ( x ) , 36.7 , 39.4 )
f7 ( x ) = f3 ( x ) + g ( f5 ( x ) - f3 ( x ) , - f4 ( x ) + f2 ( x ) , 36.7 , 39.4 )
f8 ( x ) = f2 ( x ) + g ( f6 ( x ) - f2 ( x ) , f7 ( x ) - f3 ( x ) , 49
, 65.7 )
f9 ( x ) = f3 ( x ) + g ( f7 ( x ) - f3 ( x ) , - f6 ( x ) + f2 ( x ) ,
49 , 65.7 )
x (θ, t ) = - 38 + 15 h ( t ) cosθ+ ( f2 (θ) + 38 - 15 cosθ) h ( t - 1
) + ( f8 (θ) - f2 (θ) ) h ( t - 2 ) + ( f6 (θ) - f8 (θ) ) h ( t - 3 ) +
( f2 (θ) - f6 (θ) ) h ( t - 4 ) - f2 (θ) h ( t - 5 ) + f4 (θ) h ( t - 6
)
+
( f6 (θ) - f4 (θ) ) h ( t - 7 ) + ( f4 (θ) - f6 (θ) ) h ( t - 8 ) + ( f0
(θ) - f4 (θ) ) h ( t - 9 ) - f0 (θ) h ( t - 10 ) + f0 (θ) h ( t - 11 )
+ ( - 38 + 15 cosθ- f0 (θ) ) h ( t - 12 )
y (θ, t ) = 7.8 + 15 h ( t ) sinθ+ ( f3 (θ) - 7.8 - 15 sinθ) h ( t - 1
) + ( f9 (θ) - f3 (θ) ) h ( t - 2 ) + ( f7 (θ) - f9 (θ) ) h ( t - 3 ) +
( f3 (θ) - f7 (θ) ) h ( t - 4 ) - f3 (θ) h ( t - 5 ) + f5 (θ) h ( t - 6
)
+
( f7 (θ) - f5 (θ) ) h ( t - 7 ) + ( f5 (θ) - f7 (θ) ) h ( t - 8 ) + ( f1
(θ) - f5 (θ) ) h ( t - 9 ) - f1 (θ) h ( t - 10 ) + f1 (θ) h ( t - 11 )
+ ( 7.8 + 15 sinθ- f1 (θ) ) h ( t - 12 )
参考文献:Shogo, "円と円の交点を求める", Shogo Computing Laboratory
irish052,
"テオヤンセン展", ロボットとメロディオン弾き
小川洋, "HTML5のCanvasにJavaScriptでテオ・ヤンセンのビーストを再現する", フロント・エンド・プログラミング
(2015.05.06)
正八面体
f (x) = ( |x| - |x-1| + 1 ) / 2
x ( t ) = 1 - f (t) - f (t-1) + f (t-2) + f (t-3) - f (t-4) - f (t-9) + f (t-10) + f (t-11)
y ( t ) = f (t) - f (t-1) - f (t-2) + f (t-3) - f (t-5) + f (t-6) + f (t-7) - f (t-8)
z ( t ) = f (t-4) - f (t-5) - f (t-6) + f (t-7) + f (t-8) - f (t-9) - f
(t-10) + f (t-11)
(2014.10.27)
切頭二十面体をMaximaで描く
phi:(1+sqrt(5))/2$
P:matrix([0, 1/3, phi])$
P:addrow(P,[0, -1/3, phi])$
P:addrow(P,[phi/3, -2/3, (1+2*phi)/3])$
P:addrow(P,[2*phi/3, -1/3, (2+phi)/3])$
P:addrow(P,[2*phi/3, 1/3, (2+phi)/3])$
P:addrow(P,[phi/3, 2/3, (1+2*phi)/3])$
P:addrow(P,[-phi/3, 2/3, (1+2*phi)/3])$
P:addrow(P,[-2*phi/3, 1/3, (2+phi)/3])$
P:addrow(P,[-2*phi/3, -1/3, (2+phi)/3])$
P:addrow(P,[-phi/3, -2/3, (1+2*phi)/3])$
P:addrow(P,[-1/3, -(2+phi)/3, 2*phi/3])$
P:addrow(P,[1/3, -(2+phi)/3, 2*phi/3])$
P:addrow(P,[2/3, -(1+2*phi)/3, phi/3])$
P:addrow(P,[ (2+phi)/3, -2*phi/3, 1/3])$
P:addrow(P,[ (1+2*phi)/3, -phi/3, 2/3])$
P:addrow(P,[phi, 0, 1/3])$
P:addrow(P,[ (1+2*phi)/3, phi/3, 2/3])$
P:addrow(P,[ (2+phi)/3, 2*phi/3, 1/3])$
P:addrow(P,[2/3, (1+2*phi)/3, phi/3])$
P:addrow(P,[1/3, (2+phi)/3, 2*phi/3])$
P:addrow(P,[-1/3, (2+phi)/3, 2*phi/3])$
P:addrow(P,[-2/3, (1+2*phi)/3, phi/3])$
P:addrow(P,[ -(2+phi)/3, 2*phi/3, 1/3])$
P:addrow(P,[ -(1+2*phi)/3, phi/3, 2/3])$
P:addrow(P,[-phi, 0, 1/3])$
P:addrow(P,[ -(1+2*phi)/3, -phi/3, 2/3])$
P:addrow(P,[ -(2+phi)/3, -2*phi/3, 1/3])$
P:addrow(P,[-2/3, -(1+2*phi)/3, phi/3])$
P:addrow(P,[-1/3, -phi, 0])$
P:addrow(P,[1/3, -phi, 0])$
P:addrow(P,[2/3, -(1+2*phi)/3, -phi/3])$
P:addrow(P,[ (2+phi)/3, -2*phi/3, -1/3])$
P:addrow(P,[ (1+2*phi)/3, -phi/3, -2/3])$
P:addrow(P,[phi, 0, -1/3])$
P:addrow(P,[ (1+2*phi)/3, phi/3, -2/3])$
P:addrow(P,[ (2+phi)/3, 2*phi/3, -1/3])$
P:addrow(P,[2/3, (1+2*phi)/3, -phi/3])$
P:addrow(P,[1/3, phi, 0])$
P:addrow(P,[-1/3, phi, 0])$
P:addrow(P,[-2/3, (1+2*phi)/3, -phi/3])$
P:addrow(P,[-1/3, (2+phi)/3, -2*phi/3])$
P:addrow(P,[1/3, (2+phi)/3, -2*phi/3])$
P:addrow(P,[phi/3, 2/3, -(1+2*phi)/3])$
P:addrow(P,[2*phi/3, 1/3, -(2+phi)/3])$
P:addrow(P,[2*phi/3, -1/3, -(2+phi)/3])$
P:addrow(P,[phi/3, -2/3, -(1+2*phi)/3])$
P:addrow(P,[1/3, -(2+phi)/3, -2*phi/3])$
P:addrow(P,[-2/3, -(1+2*phi)/3, -phi/3])$
P:addrow(P,[ -(2+phi)/3, -2*phi/3, -1/3])$
P:addrow(P,[ -(1+2*phi)/3, -phi/3, -2/3])$
P:addrow(P,[-phi, 0, -1/3])$
P:addrow(P,[ -(1+2*phi)/3, phi/3, -2/3])$
P:addrow(P,[ -(2+phi)/3, 2*phi/3, -1/3])$
P:addrow(P,[-1/3, -(2+phi)/3, -2*phi/3])$
P:addrow(P,[-phi/3, -2/3, -(1+2*phi)/3])$
P:addrow(P,[-2*phi/3, -1/3, -(2+phi)/3])$
P:addrow(P,[-2*phi/3, 1/3, -(2+phi)/3])$
P:addrow(P,[-phi/3, 2/3, -(1+2*phi)/3])$
P:addrow(P,[0, 1/3, -phi])$
P:addrow(P,[0, -1/3, -phi])$
A:row(P,1)$
A:addrow(A,row(P,6))$
A:addrow(A,row(P,20))$
A:addrow(A,row(P,21))$
A:addrow(A,row(P,7))$
A:addrow(A,row(P,1))$
A:addrow(A,row(P,2))$
A:addrow(A,row(P,3))$
A:addrow(A,row(P,4))$
A:addrow(A,row(P,5))$
A:addrow(A,row(P,6))$
A:addrow(A,row(P,5))$
A:addrow(A,row(P,17))$
A:addrow(A,row(P,18))$
A:addrow(A,row(P,19))$
A:addrow(A,row(P,20))$
A:addrow(A,row(P,19))$
A:addrow(A,row(P,38))$
A:addrow(A,row(P,39))$
A:addrow(A,row(P,22))$
A:addrow(A,row(P,21))$
A:addrow(A,row(P,22))$
A:addrow(A,row(P,23))$
A:addrow(A,row(P,24))$
A:addrow(A,row(P,8))$
A:addrow(A,row(P,7))$
A:addrow(A,row(P,8))$
A:addrow(A,row(P,9))$
A:addrow(A,row(P,10))$
A:addrow(A,row(P,2))$
A:addrow(A,row(P,10))$
A:addrow(A,row(P,11))$
A:addrow(A,row(P,12))$
A:addrow(A,row(P,3))$
A:addrow(A,row(P,12))$
A:addrow(A,row(P,13))$
A:addrow(A,row(P,14))$
A:addrow(A,row(P,15))$
A:addrow(A,row(P,4))$
A:addrow(A,row(P,15))$
A:addrow(A,row(P,16))$
A:addrow(A,row(P,17))$
A:addrow(A,row(P,16))$
A:addrow(A,row(P,34))$
A:addrow(A,row(P,35))$
A:addrow(A,row(P,36))$
A:addrow(A,row(P,18))$
A:addrow(A,row(P,36))$
A:addrow(A,row(P,37))$
A:addrow(A,row(P,38))$
A:addrow(A,row(P,37))$
A:addrow(A,row(P,42))$
A:addrow(A,row(P,41))$
A:addrow(A,row(P,40))$
A:addrow(A,row(P,39))$
A:addrow(A,row(P,40))$
A:addrow(A,row(P,53))$
A:addrow(A,row(P,23))$
A:addrow(A,row(P,53))$
A:addrow(A,row(P,52))$
A:addrow(A,row(P,51))$
A:addrow(A,row(P,25))$
A:addrow(A,row(P,24))$
A:addrow(A,row(P,25))$
A:addrow(A,row(P,26))$
A:addrow(A,row(P,9))$
A:addrow(A,row(P,26))$
A:addrow(A,row(P,27))$
A:addrow(A,row(P,28))$
A:addrow(A,row(P,11))$
A:addrow(A,row(P,28))$
A:addrow(A,row(P,29))$
A:addrow(A,row(P,30))$
A:addrow(A,row(P,13))$
A:addrow(A,row(P,30))$
A:addrow(A,row(P,31))$
A:addrow(A,row(P,32))$
A:addrow(A,row(P,14))$
A:addrow(A,row(P,32))$
A:addrow(A,row(P,33))$
A:addrow(A,row(P,34))$
A:addrow(A,row(P,33))$
A:addrow(A,row(P,45))$
A:addrow(A,row(P,44))$
A:addrow(A,row(P,35))$
A:addrow(A,row(P,44))$
A:addrow(A,row(P,43))$
A:addrow(A,row(P,42))$
A:addrow(A,row(P,43))$
A:addrow(A,row(P,59))$
A:addrow(A,row(P,58))$
A:addrow(A,row(P,41))$
A:addrow(A,row(P,58))$
A:addrow(A,row(P,57))$
A:addrow(A,row(P,52))$
A:addrow(A,row(P,57))$
A:addrow(A,row(P,56))$
A:addrow(A,row(P,50))$
A:addrow(A,row(P,51))$
A:addrow(A,row(P,50))$
A:addrow(A,row(P,49))$
A:addrow(A,row(P,27))$
A:addrow(A,row(P,49))$
A:addrow(A,row(P,48))$
A:addrow(A,row(P,29))$
A:addrow(A,row(P,48))$
A:addrow(A,row(P,54))$
A:addrow(A,row(P,47))$
A:addrow(A,row(P,31))$
A:addrow(A,row(P,47))$
A:addrow(A,row(P,46))$
A:addrow(A,row(P,45))$
A:addrow(A,row(P,46))$
A:addrow(A,row(P,60))$
A:addrow(A,row(P,59))$
A:addrow(A,row(P,60))$
A:addrow(A,row(P,55))$
A:addrow(A,row(P,56))$
A:addrow(A,row(P,55))$
A:addrow(A,row(P,54))$
B:matrix([0,0,0])$
B:addrow(B,A)$
B:submatrix(121,B)$
f(x):=(abs(x)-abs(x-1)+1)/2$
g[i,j]:=i*f(t-(j-1))$
C:matrix([1])$
C:addcol(C,genmatrix(g,1,119))$
D:C.(A-B)$
plot3d([D[1,1],D[1,2],D[1,3]+s],[t,0,200],[s,-0.001,0.001],[grid,200,1])$
wxMaximaではwindow枠で縦横比を調整してください。
参考文献:阿部 修, "切頭二十面体" http://www.phys.asa.hokkyodai.ac.jp/osamu/soccer/index.html
, 北海道教育大学旭川校 物理学教室 阿部ゼミ半公式ページへようこそ!
横田博史,
"はじめてのMaxima", 工学社
菅原邦雄,
"数学ソフトウェアを使ってみよう", 大阪教育大学
(2014.11.08)
サッカーボール
上から続けて、gnuplot graph画面を閉じた後、次のように入力する。
load(draw)$
draw3d( nticks = 1040, enhanced3d = true,
parametric(D[1,1]/sqrt(D[1,1]^2+D[1,2]^2+D[1,3]^2),D[1,2]/sqrt(D[1,1]^2+D[1,2]^2+D[1,3]^2),D[1,3]/sqrt(D[1,1]^2+D[1,2]^2+D[1,3]^2),t,0,130)) $
参考文献:slide_271828, "wxMaximaの使い心地(その37)常螺旋", 271828の滑り台Log
(2014.11.29)
展開図からの正四面体
f ( x ) = 1 + 3 cos x
g ( x ) = ( | x | - | x - 1 | + 1 ) / 2
f1( x , y ) = - 2 + ( - f ( x ) / 2 + 2 ) g ( y ) + ( 1 + f ( x ) / 2 )
g ( y - 1 ) + ( f ( x ) - 1 ) g ( y - 2 ) + ( 1 - f ( x ) ) g ( y - 3 )
+ ( - f ( x ) / 2 - 1 ) g ( y - 4 ) + ( - 2 + f ( x ) / 2 ) g ( y - 5 )
f2( x , y ) = ( - √(3) / 2 f ( x ) ) g ( y ) + ( - √(3) + √(3) f ( x )
/ 2 ) g ( y - 1 ) + √(3) g ( y - 2 ) + √(3) g ( y - 3 ) + ( √(3) f ( x
) / 2 - √(3) ) g ( y - 4 ) - √(3) f ( x ) g ( y - 5 ) / 2
f3( x , y ) = 3 sin ( x ) g ( y ) - 3 sin ( x ) g ( y - 1 ) + 3 sin ( x
) g ( y - 2 ) - 3 sin ( x ) g ( y - 3 ) + 3 sin ( x ) g ( y - 4 ) - 3 sin
( x ) g ( y - 5 )
f4( x ) = - 2 + 1.5 g ( x ) + 1.5 g ( x - 1 ) - 1.5 g ( x - 4 ) - 1.5 g
( x - 5 )
f5( x ) = - 0.5 √(3) g ( x ) - 0.5 √(3) g ( x - 1 ) + √(3) g ( x - 2 )
+ √(3) g ( x - 3 ) - 0.5 √(3) g ( x - 4 ) - 0.5 √(3) g ( x - 5 )
P ( - 2 + ( f4( t ) + 2 ) g ( s ) + ( f1( a , t ) - f4( t ) ) g ( s - 1 ) , f5( t ) g ( s ) + ( f2( a , t ) - f5( t ) ) g ( s - 1 ) , f3( a , t ) g ( s - 1 ) )
は
a = ±(π-Acos(1/3) ) = ±1.910… のとき正四面体
a = 0 のとき、その展開図
(2015.06.27)
曲線から渦巻線を作る
曲線が
x = x ( θ )
y = y ( θ )
0≦θ≦L
で定義されているときa、b を定数として
r ( a θ) = y (θ) ( b - x ( 0 ) ) / ( x (θ) - x ( 0 ) )
で渦巻線が定義できる。
(2011.04.09)
渦巻線の簡単な一般形
θ→x∞ で f (θ)→±∞となる関数があるとき
渦巻線は
r ( a θ) = f (θ)
となる。
参考文献:Hans Walser, 蟹江幸博 訳, "シンメトリー", 日本評論社
(2011.06.05)
輪廻転生曲線
x = r (θ) cosθ
y = r (θ) sinθ
r (θ) = sin ( aθ) + sin ( b θ) + 3
ただし、b / a は無理数とする。
参考文献:"大石進一", "フーリエ解析", "岩波書店"
(2011.10.22)
つるまきバネ記号(トロコイドの一般形)
x = a sinθ+ b θ
y = c cosθ
(2011.12.05)
|a|>|b|
(2013.09.18)
花
f ( x ) = a cos ( x )
g ( x ) = b sin ( x ) + c x
x = f (θ) cos g (θ)
y = f (θ) sin g (θ)
(2014.08.17)
つるまきバネを真横から見た場合の粗密波
つるまきバネを真横から見るとサインカーブとなるので
a ≧ b c とすると
x = a θ+ b sin(cθ- dt )
y = p sin(qθ)
参考文献:"■動画で見るFM電波と縦波の違い", "万象酔歩"
(2011.12.18)
トーラス面上のn重螺旋
閉曲線が弧長パラメータ t を用いて
x = R + x ( t )
y = y ( t )
0≦t≦L (L は周長)
と表示されているとする。( x > 0 )
この曲線を y 軸を軸に1回転してできるトーラス面上のn重螺旋はmを整数として
xk = ( R + x ( tk ( θ ) ) cosθ
yk = y ( tk ( θ ) )
zk = ( R + x ( tk ( θ ) ) sinθ
0≦θ≦2π
k = 0, 1, …, n - 1
tk ( θ ) = L { k + m θ / ( 2 π ) } / n
と表現できる。
参考文献:
小林昭七, "曲線と曲面の微分幾何", 裳華房
早苗雅史、螺旋トーラス
http://izumi-math.jp/sanae/MathCurves/MathCurves.htm
(2011.01.30)
上から見た形が断面と同じ形のトーラス面と、その面上のn重螺旋
原点を囲む閉曲線が
x = r (θ) cosθ
y = r (θ) sinθ
0≦θ≦2π
と表示されているとき
aを定数として
x = ( a r (φ) + r (θ) cosθ) cosφ
y = r (θ) sinθ
z = ( a r (φ) + r (θ) cosθ) sinφ
0≦φ≦2π
a r (φ) + r (θ) cosθ > 0
で上から見た形が断面と同じ形のトーラス面となり
この面上のn重螺旋は、
定数 b 、αk (0≦α1<α2<α3<…<αn<2π)を適当に選ぶことにより
xk = ( a r (φ) + r ( b φ + αk ) cos ( b φ + αk ) ) cosφ
yk = r ( b φ + αk ) sin ( b φ + αk )
zk = ( a r (φ) + r ( b φ + αk ) cos( b φ + αk ) ) sinφ
0≦φ≦2π
螺旋階段の手すり面と、その面上のn重螺旋
閉曲線がパラメータ t (弧長パラメータとは限らない)を用いて
x = x ( t ) = x ( t + L )
y = y ( t ) = y ( t + L )
と表示されているとすると、螺旋階段の手すり面は、
aを定数として
x = ( R (φ) + x ( t ) ) cosφ
y = a φ + y ( t )
z = ( R (φ) + x ( t ) ) sinφ
R (φ) + x ( t ) > 0
2 a π > max y ( t ) - min y ( t )
となり、この面上のn重螺旋は
xk = ( R (φ) + x ( t (φL / (2π) +αk) ) ) cosφ
yk = a φ + y ( t (φL / (2π) +αk) )
zk = ( R (φ) + x ( t (φL / (2π) +αk) ) ) sinφ
αk (0≦α1<α2<α3<…<αn<L )
t (θ) は単調関数
しめ縄面と、しめ縄螺旋
z軸の周辺に密集して互いに交わらない管が
xk = Rk(z) cosαk + rk(z) cosθ
yk = Rk(z) sinαk + rk(z) sinθ
0≦Rk(z), rk(z)
と表示されているとすると
しめ縄面はaを定数として
xk = ( Rk(z) cosαk + rk(z) cosθ) cos ( a z )
yk = ( Rk(z) sinαk + rk(z) sinθ) sin ( a z )
となり、しめ縄螺旋は
xkm = ( Rk(z) cosαk + rkm(z) cos ( bk z + βkm ) ) cos ( a z )
ykm = ( Rk(z) sinαk + rkm(z) sin ( bk z + βkm ) ) sin ( a z )
rkm(z) = ckm rk(z) ( 0≦ckm≦1 )
しめ縄で作った螺旋階段の手すり
しめ縄面はa, hを定数として
xk = Uk(θ, φ) cosφ
yk = hφ + Vk(θ, φ)
zk = Uk(θ, φ) sinφ
Uk(θ, φ) = S(φ) + ( Rk cosαk + rk cosθ) cos ( a φ)
Vk(θ, φ) = ( Rk sinαk + rk sinθ) sin ( a φ)
Uk(θ, φ) > 0
2 h π > max Vk(θ, φ) - min Vk(θ, φ)
しめ縄螺旋は
xkm = Ukm(φ) cosφ
ykm = hφ + Vkm(φ)
zkm = Ukm(φ) sinφ
Ukm(φ) = S(φ) + ( Rk cosαk + rkm cos ( bkφ + βkm ) ) cos ( a φ)
Vkm(φ) = ( Rk sinαk + rkm sin ( bkφ + βkm ) ) sin ( a φ)
Ukm(φ) > 0
2 h π > max Vkm(φ) - min Vkm(φ)
参考文献:
小林昭七, "曲線と曲面の微分幾何", 裳華房
(2011.02.27)
n重ウロボロスの蛇面と、その面上のm重螺旋
原点を囲む閉曲線が
x = r (θ) cosθ
y = r (θ) sinθ
0≦θ≦2π
と表示されているときn重ウロボロスの蛇面は
x = ( r (θ) s (φ) cosθ+ R ) cos (φ+αi )
y = r (θ) s (φ) sinθ
z = ( r (θ) s (φ) cosθ+ R ) sin (φ+αi )
0≦φ<L 、0<s (φ) 、0≦s ( L )
s (φ) は狭義の単調減少関数
この面上のm重螺旋は、
x = ( r ( ai φ+ βk ) s (φ) cos ( ai φ+ βk ) + R ) cos (φ+αi )
y = r ( ai φ+ βk ) s (φ) sin ( ai φ+ βk )
z = ( r ( ai φ+ βk ) s (φ) cos ( ai φ+ βk ) + R ) sin (φ+αi )
(2011.04.09)
月の形
x = r { 1 + ( a - 1 ) u( cosθ) } cosθ
y = r sinθ
u(x) = ( sgn(x) + 1 ) / 2
-1≦a≦1
日食の形
x = ( a * r + r cosθ) sgn( a * r + r cosθ)
y = r sinθ
-1≦a≦1
参考文献:イアン・スチュアート, "数学の秘密の本棚", ソフトバンククリエイティブ
(2010.03.20)
日食の形
上式で
x = | a * r + r cosθ|
としてもよい。
(2012.01.22)
Topへ
ヒステリシス曲線
x = cos( t )
y = - 2/3 x5 + 5/6 x3 + 5/6 x + a ( x2 - 1)2 sgn( sin( t ) ) u( t )
u(x) = ( sgn(x) + 1 ) / 2
-π/ 2 ≦ t
推奨値 a = 0.83
(2010.03.20)
富士山
y = h ( g ( |x| ) )
f (x) = ( x + |x| ) / 2
g (x) = f ( x - a ) - b
h(x) = exp( -cx )
参考文献:池田洋介, "ある静岡大学の数学入試問題について", http://iky.no-ip.org/weblog/fuji.pdf
(2012.03.20)
富士山
y = g ( exp ( - c |x| ) )
f (x) = ( x + |x| ) / 2
g (x) = - f ( -( x - a ) ) + a
(2013.02.14)
確率補正式
0≦s≦3、{ 3:間違い、1:何ともいえない、0:正解に近い} とするときの確率 p の補正式
f(s,p) = 2(s -1)p3 - 3(s -1)p2 + sp
-1≦t≦1、{ -1:間違い、0:何ともいえない、1:正解に近い} とするときのt から s への変換式
s(t) = t2 /2 - 3t /2 + 1
(2009.07.25)
確率補正式(フェルミ分布関数の応用)
0≦s≦1、{ 0:間違い、1:正解 } とするときの確率 p の補正式
f(s,p) = 1 / [ exp { s ( 2 p - 1 ) / ( s - 1 ) } + 1 ]
-1≦t≦1、{ -1:間違い、1:正解 } とするときのt から s への変換式
s(t) = a ( 1 + t ) / ( 1 - t )
推奨値 a = 2/3、3/4、0.87
参考文献:"和達三樹"、"十河 清"、"出口哲生", "ゼロからの熱力学と統計力学", "岩波書店"
(2010.05.16)
f ( s, 0 ) の値を
100分の1以下にする場合、 a = 0.83
1000分の1以下にする場合、a = 0.88
1万分の1以下にする場合、 a = 0.91
100万分の2以下にする場合、a = 0.93
(2010.08.28)
デルタ関数
上の関数はs → 1- で ヘビサイド関数 u ( x - 1/2 ) となり、
その微分はディラックのデルタ関数δ( x - 1/2)となる。
両方とも初等関数の極限として表すことができる。
参考文献:"大石進一", "フーリエ解析", "岩波書店"
"和達三樹"、"十河清"、"出口哲生", "ゼロからの熱力学と統計力学", "岩波書店"
(2011.11.20)
確率補正式
上式で
f(s,p) = Atan( ( x - 1/2 ) / ( 1/s - 1 ) ) / π + 1/2
としてもよい。
(2011.11.20)
確率補正式
f ( p ) が [ 0 , 1 ] で有界のとき
g ( p , m ) = { f ( p ) + u ( p - m ) - sgn ( p - m )|f ( p ) - u ( p - m )|} / 2
ただし、0≦m≦1 のとき -1/2≦f ( m )≦3/2
p = m での連続性を保証する場合 lim { p →m } f ( p ) = 1/2 、f ( m ) = 1/2
u(x) = ( sgn(x) + 1 ) / 2
(2010.06.20)
方形波を連続関数で近似する
a は1に十分近く a<1とする。
f ( x ) = { 1 - exp ( a x / ( a - 1 ) ) } / { 1 + exp ( a x / ( a - 1 ) ) }
方形波は-1<c<1として以下で近似する
y = f ( cos ( 2 π x - b t ) - c )
この関数はフーリエ級数のようなギブス現象は発生せず
a → 1 で方形波の定義式に一致する。
参考文献:"大石進一", "フーリエ解析", "岩波書店"
"和達三樹"、"十河清"、"出口哲生", "ゼロからの熱力学と統計力学", "岩波書店"
(2011.11.13)
方形波を連続関数で近似する
上式で
f ( x ) = 2 Atan( a x / ( 1 - a ) ) / π
としてもよい。
(2011.11.20)
第1、第3 四分位点を通る関数
f ( x, a, b ) = 1 / [ 1 + exp { -2 * log 3 * ( x - ( a + b ) / 2 ) / ( b - a ) } ]
a は第1 四分位点 、b は第3 四分位点とする。
(2011.10.08)
第1、第3 四分位点を通る関数
上式で
f ( x, a, b ) = atan( 2 * ( x - ( a + b ) / 2 ) / ( b - a ) ) / π + 1/2
としてもよい。
(2011.11.20)
3つの四分位点を通る関数をMaximaで作る
X1<x2<x3、x1が25%点 、x2が中央値、x3が75%点とする。
x0<X1のとき0<y0<0.25は0に近い値、
X3<x0のとき0.75<y0<1は1に近い値とする。
h1(x) := 1 / (2*( exp(-a *( x-b)) + 1) ) + 1 /(2*( exp(-c *( x-d)) + 1) );
eq(x0,y0,x1,x2,x3):=[h1(x0)-y0, h1(x1)-0.25, h1(x2)-0.5, h1(x3)-0.75];
m(F,x0,y0,x1,x2,x3):=block([eql],
eql : eq(x0,y0,x1,x2,x3),
return( apply(F,[eql,[a,b,c,d], [1,x1,1,x3]]) ) )$
h2(x,m):=1 /(2*( exp (-rhs((m[1])[1]) *( x-rhs((m[1])[2]))) + 1) ) + 1 /(2*( exp(-rhs((m[1])[3]) *( x-rhs((m[1])[4]))) + 1)) ;
load("mnewton")$
( 0, 0.001), ( 5, 0.25 ), ( 10, 0.5 ), ( 12, 0.75 )を通る関数は下記のように定義する。
f(x):= h2(x,m('mnewton,0,0.001,5,10,12));
参考文献:
市川雄二, "Maxima 5.25.1 Manual", 市川雄二のホームページ
http://www.h3.dion.ne.jp/~y.ich/Maxima/maxima_68.html
横田博史, "Maxima Manual", 狸穴
http://www.bekkoame.ne.jp/~ponpoko/Math/maxima/maxima_7.html#SEC28
赤間世紀, "Maximaで学ぶコンピュータ代数", 工学社
(2011.10.08)
3つの四分位点を通る関数をExcel 2007のソルバーで作る(5点指定)
Excel 2007のソルバーの起動方法はヘルプを参照しください。
まず、シート全体の書式を数値で小数点以下30桁まで表示にしてください。
A1セルに
=D$1/(EXP(-D$2*(C1-D$3))+1)+D$4/(EXP(-D$5*(C1-D$6))+1)
と入力し、A1セルをコピーしてA2~A5セルに貼り付けてください。
B1~B5セルをy座標値として0.001, 0.25, 0.5, 0.75, 0.999 を順番に入力してください。
C1~C5セルをx座標値とし例題として0, 5, 10, 12, 13 を順番に入力してください。
D1~D6セルに仮の値(この例題では全て1でよい)を入力してください。
ソルバー:パラメータ設定 画面を開き
目的セル:$A$1
目標値の値:0.001
変化させるセル:$D$1:$D$6
制約条件:
$A$2 = $B$2
$A$3 = $B$3
$A$4 = $B$4
$A$5 = $B$5
$D$1 = 1-$D$4
と入力し実行ボタンを押す。
「最適解が見つかりました。」とメッセージが出たら成功。
解を記入するを選択しOKボタンを押す。
求める関数は
f ( x ) = D1 / ( exp ( -D2 ( x - D3 ) ) + 1 ) + D4 / ( exp ( -D5 ( x - D6 ) ) + 1 )
ただし、D1, D2, D3, D4, D5, D6はExcel のセルの値。
この例題ではソルバーのオプションは初期設定のままでよい。
初期設定値はヘルプに書いてないのでここに記す。
制限時間:100秒
反復回数:100
精度:0.000001
公差:5%
収束:0.0001
近似方法:一次式
微分係数:前進
探索方法:準ニュートン法
その他のオプションは全てOFF
参考文献:
"有限会社ゴッドフット企画", "エクセルのソルバーを用いた非線形連立方程式の計算
", "有限会社ゴッドフット企画"
(2011.10.22)
3つの四分位点を通る関数をExcel 2007のソルバーで作る(3点指定)
まず、シート全体の書式を数値で小数点以下30桁まで表示にしてください。
A1セルに
=D$1/(EXP(-D$2*(C1-D$3))+1)+D$4/(EXP(-D$5*(C1-D$6))+1)
と入力し、A1セルをコピーしてA2, A3セルに貼り付けてください。
A4セルに
=(D$4*D$5*EXP(-D$5*(C1-D$6)))/(EXP(-D$5*(C1-D$6))+1)^2+(D$1*D$2*EXP(-D$2*(C1-D$3)))/(EXP(-D$2*(C1-D$3))+1)^2
と入力し、A4セルをコピーしてA5, A6セルに貼り付けてください。
A7セルに
=MAX(A4,A5,A6)-MIN(A4,A5,A6)
と入力してください。
B1~B3セルをy座標値として0.25, 0.5, 0.75を順番に入力してください。
C1~C5セルをx座標値とし例題として5, 10, 12を順番に入力してください。
D1~D6セルに仮の値を(この例題では0.5, 1, 5, 0.5, 1, 12を順番に)入力してください。
ソルバー:パラメータ設定 画面を開き
目的セル:$A$7
目標値:最小値
変化させるセル:$D$1:$D$6
制約条件:
$A$1 = $B$1
$A$2 = $B$2
$A$3 = $B$3
$D$1 = 1-$D$4
と入力し実行ボタンを押す。
「最適解が見つかりました。」とメッセージが出たら成功。
解を記入するを選択しOKボタンを押す。
求める関数は
f ( x ) = D1 / ( exp ( -D2 ( x - D3 ) ) + 1 ) + D4 / ( exp ( -D5 ( x - D6 ) ) + 1 )
ただし、D1, D2, D3, D4, D5, D6はExcel のセルの値。
この例題ではソルバーのオプションは初期設定のままでよい。
(2011.10.23)
ステンレスの壁面を流れ落ちる細い水の流れのモデル
x = f ( y, t ) = Σ{n=0~∞} an(t) / [ 1 + exp { bn(t) * ( y - cn(t) ) } ]
(2011.10.08)
a 個のものを b 日間で処理する
処理のピークが bc 日目(1/2 ≦ c ≦ 1)にくるとき
t 日目の処理個数は
f ( t ) = - 3 a { ( t / b - c )2 - c2 } / { b ( 3 c - 1 ) }
(2010.02.15)
t 日目までの処理完了数は
F ( t ) = - a { ( t / b )3 - 3 c ( t / b )2 } / ( 3 c - 1 )
(2010.06.05)
a 個のものを b 日間で処理する
f ( t ) を区間 [0 1] で単調関数、f ( 0 ) ≠ f ( 1 ) とするとき
t 日目の処理個数は
g ( t ) = a f ' ( t / b ) / { f ( 1 ) - f ( 0 ) }
(2010.05.22)
t 日目までの処理完了数は
G ( t ) = a { f ( t / b ) - f ( 0 ) } / { f ( 1 ) - f ( 0 ) }
(2010.06.05)
S 個のものを D 日間で処理する
前回の実績が総数 a 個、工数 b 日間、t 日目の処理個数が f ( t ) のとき
今回の t 日目の処理個数は
g ( t ) = S b f ( b t / D ) / ( a D )
(2010.05.29)
今回のt 日目までの処理完了数は
G ( t ) = S F ( b t / D ) / a , F ( x ) = ∫[0, x] f ( u ) du
(2010.06.05)
上式で F ( x ) を前回のt 日目までの処理完了数と定義してもよい。
前回実績を表わす関数はスプライン関数や回帰曲線等を使用する
参考文献:桜井 明, "スプライン関数入門",東京電機大学出版局
(2010.06.20)
四分位点を通る関数も使える。
(2011.10.08)
S 個のものを D 日間で処理する
1日の最小処理個数を m 個、
1日の最大処理個数を M 個とする。
初日の処理個数を m 個とし、処理個数を線形に増やしていき
d 日目以降は毎日 M 個処理するとすると
d = 2 ( D M - S ) / ( M - m )
t 日目の処理個数は
d 日目まで
g ( t ) = ( M - m ) t / ( d - 1 ) + m - ( M - m ) / ( d - 1 )
(2011.10.09)
S 個のものを D 日間で処理する(d 日目からテコ入れ開始)
1日の最小処理個数を m 個、
1日の最大処理個数を M 個とする。
1日目の処理個数を m 個とし、処理個数を1日a個づつ増やしていくと
d 日目は m + a ( d - 1 ) 個処理することになる。
D 日目の処理個数が M 個になるようにd 日目以降の処理個数を線形に増やしていくとすると
{ m + m + a ( d - 2 ) } ( d - 1 ) / 2 + { M + m + a ( d - 1 ) } ( D - d + 1 ) / 2 = S
が成り立つ。
(2011.10.15)
Maximaで s 個のものを d 日間で処理する計画を立てる
f(x,a):=Upper_confidence_limit(2*x-1,a,-a)/2+1/2$
g(x):=(37*x^3-137*x+100)/200$
Upper_confidence_limit は上で定義した上側信頼限界曲線を求める関数。
1日の最小処理個数を n 個、
1日の最大処理個数を m 個とするとき
x 日目( 1 < x < d )の処理個数を以下で計算する。
h(x,s,d,n,m):=(m-n)*f((x-1)/(d-1),find_root(g(a)-(s-n*d)/((m-n)*d)=0, a, -1.1, 1.1))+n$
(2011.11.6)
s 個のものを d 日間で処理する計画を立てる
1日の最小処理個数を n 個、
1日の最大処理個数を m 個とするとき
x 日目( 1 ≦ x ≦ d )の処理個数を以下で計算する。
h ( x, s, d, n, m ) = ( m - n ) g( ( x - 1 ) / ( d - 1 ), ( s - n d ) / { ( m - n ) d } ) + n
g ( x, a ) = ( 1 - a ) f( x - 1 + a ) / a - a f( - x + 1 - a ) / ( 1 - a ) + a
f ( x ) = ( x + |x| ) / 2
nd < s < md
(2013.06.29)
Maximaで進捗率の補正をする
f(x,a):=50*Upper_confidence_limit(x/50-1,0,(a-50)/50)+50$
Upper_confidence_limit は上で定義した上側信頼限界曲線を求める関数。
0≦x≦100(%)
0<a<100(%)
x は、補正したい進捗率(%)
a は、進捗率50%とする報告日が実績日数の a % くらいになる傾向があるということ
a を上と同じとし、x 日目に進捗率 y % と報告された場合、あと何日で完成するかを計算する関数は以下で定義する。
g(x,y,a):=x*(100/f(y,a)-1)$
(2013.06.15)
進捗率 b %とする報告日が実績日数の c % くらいになる傾向があるときは
f(x,b,c):=50*Upper_confidence_limit(x/50-1,(b-50)/50,(c-50)/50)+50$
(2013.06.22)
嘘つき文に論理矛盾はない
(証明)
1.嘘つき文は真偽を決定できないため命題ではない。
2.よって古典論理の適用対象外である。
証明終わり
(2012.03.30)
Ushenkoのパラドックス
↓枠A
| 枠A内の文は偽 |
枠A内の文が真であると仮定すると枠A内の文から枠A内の文は偽となり矛盾する。つまり枠A内の文は偽。
枠A内の文が偽であるため、真となる(枠A内の文の否定)文が存在することになるが枠A内には文が一つしかないから枠A内の文の否定文は枠Aの外に存在する。
枠A外の文「枠A内の文は偽」は枠A内の文の否定文である。そして枠A外の文「枠A内の文は真」は枠A内の文と同値となる。
枠A内に文が一つしかないため枠A内の文を枠A外に取り出すことができた。めでたし めでたし。
参考文献:鈴木真奈, "<一般論文>A. P. Ushenko の単純嘘つき文の議論に見る真理概念の哲学的分析の歴史",京都大学
嘘つき文がパラドックスと誤認される理由
文A0:「文A0は偽」
文A0が真と仮定すると文A0の内容から文A0は偽となり矛盾する。
よって文A0は偽となり、文A0の否定文が真となる。(文A0は文A0の否定文になりえない)
文A1:「文A0は偽」
文A1が偽と仮定すると文A0が真となり文A0の内容から文A0は偽となり矛盾する。
よって文A1は真であり、文A0の否定文である。
文A1は文A0の否定文であるにもかかわらず、文面が同じなので文A1と文A0は同じ文であると錯覚し
嘘つき文がパラドックスであると誤認される。
嘘つき文がパラドックスとなるためには「同じ文面の文は同じ文である」という公理を追加する必要がある。
(2015.11.30)
文B0:「文B0は真」
文B0は真でも偽でも矛盾しないため命題ではない。
(2016.08.20)
「私は嘘つき」という発言はパラドックス
人A0:「人A0は嘘つき」
人A0が正直者と仮定すると人A0の発言内容から人A0は嘘つきとなり矛盾する。
よって人A0は嘘つきとなり、人A0の発言内容の否定文が真となる。(つまり人A0は正直者となり最初の仮定に戻ってしまう)
(2016.08.13)
多重人格であると認識している正直人格なら発言できる
正直人格と嘘つき人格による多重人格者で、人格は発言中に変わらないとする。
「あなたは嘘つきですか?」と質問された場合
| No | 多重人格と認識して | 人格 | 振る舞い |
| 1 | いる | 正直 | 「嘘つき人格の時は嘘つきですが今は正直です」 |
| 2 | ない | 正直 | 「いいえ、私は正直です」 |
| 3 | いる | 嘘つき | No1として発言すると、多重人格と認識していることになるため発言不可能。 「いいえ、私は正直です」と発言すると、「No1でない」と本当のことを言うのと同値になり発言不可能。 質問内容がわからないなど、これら以外の発言をすると、No3であると特定されるため、多重人格と認識している嘘つきは論理的に存在しない。 |
| 4 | ない | 嘘つき | 「いいえ、私は正直です」 |
「私は嘘つき」と発言する場合
| No | 多重人格と認識して | 人格 | 振る舞い |
| 1 | いる | 正直 | 「私は(嘘つき人格の時は)嘘つき」 |
| 2 | ない | 正直 | 嘘を言ってしまうため発言不可能 |
| 3 | いる | 嘘つき | - |
| 4 | ない | 嘘つき | 本当のことを言ってしまうため発言不可能 |
(2017.02.05)
上で、人格は発言中に変わらないではなく、質問開始から回答完了までの間、人格が変わらないでした。
(2020.06.14)
「真であるが、真であることを証明できない文」(文Aとする)を判定する文は存在しない
判定文Bがそのような判定文とすると、文Aは判定文Bにより真であることが証明されるが、
文Aが真であることを証明できない文であることと矛盾する。
(2016.07.15)
「この文は矛盾する。」
という文は偽。なぜならば真だとすると矛盾することになるから。
(2012.12.08)
カリーのパラドックスは古典論理の命題の系
カリーのパラドックスとは「この文が真なら1=0は真」という文から1=0が真と結論できるとする主張であるが
古典論理では前件が偽なら後件は真でも偽でも良いので、間違った結論が導かれたということは前件が偽
つまり「この文」は偽、ということは「この文が真なら1=0は偽」が真ということになる。
このように「この文が真なら命題Aが成り立つ」という文は命題Aの真偽と一致する。
「この文が真なら、(この文は)真」という文は真
「この文が真なら、(この文は)偽」という文は偽
逆に言うと古典論理の命題では「この文が真なら」という文が省略されているとも言える。
参考文献: "カリーのパラドックス",ウィキペディア フリー百科事典
(2013.10.28)
「この文が真なら1=0は真」の対偶をとると「1=0が偽ならこの文は偽」。つまり、「1=0が偽ならこの文は真」が真になる。
(2013.11.06)
「この文が命題ならば、この文は偽」
という文は偽。なぜならば、この文が真であると仮定すると、この文は偽となり、真であると仮定したことと矛盾する。
「この文が真ならば、この文は命題ではない」
という文は偽。なぜならば、この文が真であると仮定すると、この文は真偽を決定できないことになり、真であると仮定したことと矛盾する。
「この文は命題である」
という文は真。なぜならば、この文が偽であると仮定すると、この文は真偽を決定できないことになり、偽であると仮定したことと矛盾する。
「この文が真ならば、この文は命題である」
という文は真。なぜならば、この文が偽であると仮定すると、この文の前件が偽となり、この文は真となるが、これは偽であると仮定したことと矛盾する。
「この文が命題ならば、1=0は真」
という文は偽。この文の対偶「1=0が偽ならば、この文は命題ではない」を真とすると、左の文は真偽を決定できないことになり、真であると仮定したことと矛盾する。
自明のことであるが、古典論理の命題では「この文が命題ならば」という文が省略されている。
(2014.12.27)
C:「この文がAならば、この文はB」の真理表
| No | A | B | Cの真理値 | 証明 | Cの対偶No | Cの対偶の真理値 | Cの否定No | Cの否定の真理値 | ルーツNo |
| 1 | 偽 | 偽 | 命題であり真 | No6の対偶であるから。 | 6 | 命題であり真 | 2 | 命題ではない | 6,5 |
| 2 | 偽 | 真 | 命題ではない | Cを真と仮定するとCの前件が偽となりCは真。よって矛盾しない。 一方Cを偽と仮定するとNo1が真となり矛盾しない。 Cは真と仮定しても偽と仮定しても矛盾しないのでCは命題ではない。 |
2 | 命題ではない | 1 | 命題であり真 | 1,6,5 |
| 3 | 偽 | 命題 | 命題ではない | No14の対偶であるから。 | 14 | 命題ではない | 4 | 命題であり真 | 14,13,7,8 |
| 4 | 偽 | 命題でない | 命題であり真 | No10の対偶であるから。 | 10 | 命題であり真 | 3 | 命題ではない | 10,9 |
| 5 | 真 | 偽 | 命題であり偽 | Cを真と仮定するとCの後件からCは偽となり矛盾。 | 5 | 命題であり偽 | 6 | 命題であり真 | 5 |
| 6 | 真 | 真 | 命題であり真 | Cを偽と仮定するとNo5が真になる。No5の後件からNo5は偽となり矛盾。 | 1 | 命題であり真 | 5 | 命題であり偽 | 5 |
| 7 | 真 | 命題 | 命題であり真 | Cを偽と仮定するとNo8が真となり矛盾。 | 13 | 命題であり真 | 8 | 命題であり偽 | 8 |
| 8 | 真 | 命題でない | 命題であり偽 | Cを真と仮定するとCは命題ではないことになるが、これはCを真と仮定したことに反する。 | 9 | 命題であり偽 | 7 | 命題であり真 | 8 |
| 9 | 命題 | 偽 | 命題であり偽 | Cを真と仮定するとCは偽になるが、これはCが真と仮定したことに反する。 | 8 | 命題であり偽 | 10 | 命題であり真 | 9 |
| 10 | 命題 | 真 | 命題であり真 | Cを偽と仮定するとNo9が真となり矛盾。 | 4 | 命題であり真 | 9 | 命題であり偽 | 9 |
| 11 | 命題 | 命題 | 命題であり真 | Cを偽と仮定するとNo12が真となり矛盾。 | 16 | 命題であり真 | 12 | 命題であり偽 | 12 |
| 12 | 命題 | 命題でない | 命題であり偽 | Cを真と仮定するとCは命題ではないことになるが、これはCを真と仮定したことに反する。 | 12 | 命題であり偽 | 11 | 命題であり真 | 12 |
| 13 | 命題でない | 偽 | 命題であり真 | No7の対偶であるから。 | 7 | 命題であり真 | 14 | 命題ではない | 7,8 |
| 14 | 命題でない | 真 | 命題ではない | Cを真と仮定するとCの前件が偽となりCは真。よって矛盾しない。 一方Cを偽と仮定するとNo13が真となり矛盾しない。 Cは真と仮定しても偽と仮定しても矛盾しないのでCは命題ではない。 |
3 | 命題ではない | 13 | 命題であり真 | 13,7,8 |
| 15 | 命題でない | 命題 | 命題ではない | Cを真と仮定するとCの前件が偽となりCは真。よって矛盾しない。 一方Cを偽と仮定するとNo16が真となり矛盾しない。 Cは真と仮定しても偽と仮定しても矛盾しないのでCは命題ではない。 |
15 | 命題ではない | 16 | 命題であり真 | 16,11,12 |
| 16 | 命題でない | 命題でない | 命題であり真 | No11の対偶であるから。 | 11 | 命題であり真 | 15 | 命題ではない | 11,12 |
(2015.1.11)
四則演算で論理演算を実行する
A 、B を { -1:偽 、1:真 } をとる二値論理式とするとき
f (A , B , n ) = { A + B + (-1)n ( 1- AB ) } / 2
n が奇数なら論理積
n が偶数なら論理和
(2009.07.25)
確率論的論理学との関係
永井俊哉氏の確率論的論理学の否定、連言、選言式にp = (A + 1) / 2、q = (B + 1) / 2 を代入し
結果を2倍して1引くと上式が導かれるため、多値論理に拡張可能。
(2009.08.08)
n 変数の場合
-1 ≦ X1, X2, …, Xn ≦ 1 とする。
f(X1, X2, …, Xn, m ) = (-1)m [ Π{k=1~n} { (-1)m Xk + 1 } - 2n-1 ] / 2n-1
m が奇数なら X1 ∨ X2 ∨ … ∨ Xn
m が偶数なら X1 ∧ X2 ∧ … ∧ Xn
(2009.08.30)
真理値区間が[a b]の場合
X1, X2, …, Xn を区間[a b]を真理値(a は偽、b は真)とする論理変数とする。
否定式: - X + a +b
f(X1, X2, …, Xn, s, t ) = s + Π{k=1~n} ( Xk - s ) / ( t - s )n-1
s = a, t = b なら X1 ∧ X2 ∧ … ∧ Xn
s = b, t = a なら X1 ∨ X2 ∨ … ∨ Xn
(2009.09.13)
a は真、b は偽 とすると
s = a, t = b なら X1 ∨ X2 ∨ … ∨ Xn
s = b, t = a なら X1 ∧ X2 ∧ … ∧ Xn
(2009.09.20)
g ( t ) を区間 [ a, b ] で単調関数、f ( a ) ≠ f ( b ) とするとき
否定式を
a + ( b - a ) { g ( X ) - g ( a ) } / { g ( b ) - g ( a ) }
としてもよい。
(2010.05.30)
真理値区間が[ a, b ]の場合の結果を、Kleeneの強3値論理に変換する
( 1 - r ) a + r b ( 0 < r < 1 ) を真偽不明の真理値と定義する。
g ( x ) = ( b - a ) { ( 1 - r ) sgn2 ( x - a ) - r sgn2 ( x - b ) } + ( 1 - r ) a + r b
x = f ( X1, X2, …, Xn, s, t )
(2010.08.28)
参考文献:赤間世紀, 宮本定明, "ソフトコンピューティングのロジック", 工学社, (2008)
(2010.12.11)
確率論的論理学の逆説とファジィ論理
確率論的論理学の真理値を
{ p = 0:間違い、0<p <0.5:間違いかも知れない、p = 0.5:どちらとも言えない、0.5<p <1:正しいかも知れない、p = 1:正しい } とすると、
「どちらとも言えない」かつ「どちらとも言えない」は「間違いかも知れない」
「どちらとも言えない」または「どちらとも言えない」は「正しいかも知れない」となり
なんとなく直観と相容れない気がする。
一方、現在実用化されているファジィ論理では2つとも「どちらとも言えない」となり感覚的であり、まさにファジィである。
(2009.08.08)
参考文献:大窪徳行・和田和行 編著, "21世紀の論地", 八千代出版, (2007)
(2010.10.09)
システムの信頼度計算にファジィ論理は使えない
システムの信頼度計算では確率論的論理学が成立している。
(2009.08.16)
参考文献:大村 平, "信頼性工学のはなし", 日科技連, (1988)
(2009.10.04)
確率論的論理学の逆説は、なぜ生じたか?
上記の逆説は真理値に客観的な確率値ではなく感覚的な意味を与えたため生じたことがわかる。
そのため、感覚を扱うのが得意なファジィ論理の方がしっくりくるのである。
(2009.08.16)
区間外にも真理値を
その点から2境界点までの距離の比(外分比)と同じ比率で区間内に点(内分点)をとり、その真理値を区間外の点の真理値とする。
(2009.08.08)
n次元ユークリッド空間上に拡大
上記方法で拡張する。
2次元の場合、同じアポロニウスの円上の点は同じ真理値となる。
(2009.08.16)
電気回路論理(抵抗値論理、インダクタンス論理、キャパシタンス論理)
信頼度計算と確率論的論理学を比較すると
直列は連言式、並列は選言式に対応し、ド・モルガンの法則が成立している。
そのアナロジーを抵抗値計算に適用すると抵抗値論理を定義できる。
この場合、真理値は正の実数で R > 0
否定式は 1/R
連言式(直列回路)はR1+R2
選言式(並列回路)は 1/(1/R1 + 1/R2)
となり、ド・モルガンの法則が成立している。
ブリッジの扱い
回路上にブリッジがある場合は事前にΔ-Y変換を使って直並列回路に変換する必要がある。
参考文献:関根松夫, "やさしい電気回路", 昭晃堂, (2005)
最短経路長論理
最短経路長を求める計算から最短経路長論理を定義する。
この場合、真理値は正の実数で R ≧ 0
否定式は存在しない。
連言式(直列路)は R1 + R2
選言式(並列路)は min(R1, R2)
となり、ド・モルガンの法則は成立しない。
ブリッジは一緒に計算可能。
グラフ最大流量論理(ブリッジがない場合)
ブリッジのない(直並列路のみの)グラフ最大流量計算からグラフ最大流量論理を定義する。
この場合、真理値は正の実数で R ≧ 0
否定式は存在しない。
連言式(直列路)は min(R1, R2)
選言式(並列路)は R1 + R2
となり、ド・モルガンの法則は成立しない。
(2009.09.06)
グラフ最大流量論理(一般の場合)
最大フロー最小カット定理により
グラフ最大流量論理のグラフの双対グラフを作り、最短経路長論理を適用すると、グラフ最大流量が決定できる。
参考文献:E.クライツィグ, "最適化とグラフ理論", 培風館
斎藤伸自, 西関隆夫, 千葉則茂, "離散数学", 朝倉書店
(2009.09.20)
グラフ最小流路容量論理
グラフ内で最小流量の流路を1本決定し、その容量をもとめる計算から、グラフ最小流路容量論理を定義する。
この場合、真理値は正の実数で R ≧ 0
連言式(直列路)は min(R1, R2)
選言式(並列路)は min(R1, R2)
否定式をR(真理値が変化しない)とすると
ド・モルガンの法則が成立する。
ブリッジは一緒に計算可能。
グラフ最大流路容量論理(ファジィ論理)
グラフ内で最大流量の流路を1本決定し、その容量をもとめる計算から、グラフ最大流路容量論理を定義する。
この場合、真理値は正の実数で R ≧ 0
連言式(直列路)は min(R1, R2)
選言式(並列路)は max(R1, R2)
グラフの辺の最大容量をRmaxとすると
否定式は Rmax - R
となり、ド・モルガンの法則が成立する。
ブリッジは一緒に計算可能。
特に、Rmax = 1 のときファジィ論理に一致する。
(2009.09.13)
3点(a,b)、(c,d)、(m,n)を通る折れ線(a<c<m)
f ( x ) = ( |x| + x ) / 2
g ( x ) = d - ( d - b ) f ( - ( x - c ) ) / ( c - a ) + ( n - d ) f ( x - c ) / ( m - c )
(2016.1.23)
最小試行回数
ある事象が発生する経験的確率がp (0 < p < 1)で
試行回数が不明な時、次式で最小試行回数を求める。
f (p) = 2 / ( 1 - | 2p - 1| )
p = 0, 1 のときの最小試行回数は1回です。
(2011.12.31)
冗談コーナー釣堀 (○んちテーゼ)
壊れかけのプロパガンダ再生工場
クリストッフェルの記号 Γλμν を以下のように定義する。
Ch_sym( g, cv, lam, mu, nu) := block( [sum],
sum : 0,
for rho : 0 thru 3 do( sum : sum + invert( g )[lam + 1, rho + 1] * ( diff( g[rho + 1, nu + 1], cv[mu + 1] ) + diff( g[mu + 1, rho + 1], cv[nu + 1] ) - diff( g[mu + 1, nu + 1], cv[rho + 1] ) ) ),
return( sum / 2 ))$
パラメータの意味は、Ch_sym( g = 計量行列, cv = 座標変数の組, lam = λ, mu = μ, nu = ν);
ただし、λ, μ, ν は 0 ~ 3 の整数
g は4×4の正方行列
cv は4次元ベクトル
例えば、フリードマン-ロバートソン-ウォーカー計量
ds2 = - c2 dt2 + a ( t )2 { dr2 / ( 1 - k r2 ) + r2 dθ2 + r2 sin2θ dφ2 }
の場合、計量行列を以下で定義する。
g : matrix( [-c^2, 0, 0, 0], [0, a(t)^2 / ( 1 - k * r^2 ), 0, 0], [0, 0, a(t)^2 * r^2, 0], [0, 0, 0, a(t)^2 * r^2 * sin( theta )^2]);
座標変数の組は以下で定義する。
cv : [t, r, theta, phi];
Γrt r は以下のように計算する。
Ch_sym( g, cv, 1, 0, 1);
Γθrθ 、Γφθφ はそれぞれ以下のように計算する。
Ch_sym( g, cv, 2, 1, 2);
Ch_sym( g, cv, 3, 2, 3);
参考文献:窪田高弘、佐々木 隆, "相対性理論", 裳華房
赤間世紀, "Maximaで学ぶコンピュータ代数", 工学社
足立健朗, "maxima による行列計算超入門", http://www.yo.rim.or.jp/~kenrou/maxima/maximaintro.pdf
(2010.08.06)
Topへ
クリストッフェルの記号 Γλμν は上記で定義する。
リーマンの曲率テンソルを以下で定義する。
Riemann_curvature_tensor( g, cv, mu, alpha, beta, gamma ) := block( [sum],
sum : diff( Ch_sym( g, cv, mu, alpha, gamma ), cv[beta + 1] ) - diff( Ch_sym( g, cv, mu, alpha, beta ), cv[gamma + 1] ),
for lambda : 0 thru 3 do( sum : sum + Ch_sym( g, cv, mu, lambda, beta ) * Ch_sym( g, cv, lambda, alpha, gamma )
- Ch_sym( g, cv, mu, lambda, gamma ) * Ch_sym( g, cv, lambda, alpha, beta )
),
return( sum ))$
リッチテンソルを以下で定義する。
Ricci_tensor( g, cv, alpha, beta ) := block( [sum],
sum : 0,
for mu : 0 thru 3 do( sum : sum + Riemann_curvature_tensor( g, cv, mu, alpha, mu, beta )
),
return( sum ))$
スカラー曲率を以下で定義する。
scalar_curvature( g, cv ) := block( [sum],
sum : 0,
for alpha : 0 thru 3 do(
for beta : 0 thru 3 do(sum : sum + invert(g)[alpha + 1, beta + 1] * Ricci_tensor( g, cv, alpha, beta )
)),
return( sum ))$
ロバートソン-ウォーカー計量
ds2 = - dt2 + a ( t )2 { dx2 / ( 1 - K x2 ) + x2 dθ2 + x2 sin2θ dφ2 }
の計量行列を以下で定義する。
g : matrix( [-1, 0, 0, 0], [0, a(t)^2 / ( 1 - K * x^2 ), 0, 0], [0, 0, a(t)^2 * x^2, 0], [0, 0, 0, a(t)^2 * x^2 * sin( theta )^2]);
座標変数の組は以下で定義する。
cv : [t, x, theta, phi];
アインシュタイン方程式の計量が関係する項の(0,0)成分は以下のようになる。
ratsimp(Ricci_tensor( g, cv, 0, 0 ) - scalar_curvature( g, cv ) * g[1,1] / 2 + lam * g[1,1]);
エネルギー運動量テンソル(完全流体)の(0,0)成分は以下のように評価する。
u : [1, 0, 0, 0];
( rho + p ) * u[1] * u[1] + p * g[1, 1];
参考文献:須藤 靖, "一般相対論入門", 日本評論社
松田卓也、二間瀬敏史, "なっとくする相対性理論", 講談社
(2010.08.10)
Topへ
ラグランジュの運動方程式で一般化力を除いた部分 d/dt (∂L / ∂qi' ) - ∂L / ∂qi を以下のように定義する。
Lagranges_equations_of_motion( gc, Lagrangian, i ) :=
ratsimp( diff( diff( Lagrangian, diff( gc[i], t ) ), t ) - diff( Lagrangian, gc[i] ) )$
パラメータの意味は、Lagranges_equations_of_motion( gc = 一般化座標の組, Lagrangian = ラグラジアン, i = 一般化座標の添字 );
ただし、
gc はベクトル
i は 1以上で gc の次元以下の整数
倒立振り子系の一般化座標を以下で定義する。
gc : [z( t ), theta( t )];
系の運動エネルギTを以下で定義する。
T : ( M * ( diff( z( t ), t ) )^2 + m * ( ( diff( z( t ), t ) + L * diff( theta( t ), t ) * cos( theta( t ) ) )^2 + ( L * diff( theta( t ), t ) * sin( theta( t ) ) )^2 ) + J * diff( theta( t ), t )^2 ) / 2;
系の位置エネルギUを以下で定義する。
U : m * g * L * cos( theta( t ) );
系の一般化力を除いた部分の式は
Lagranges_equations_of_motion( gc, T - U, 1 );
Lagranges_equations_of_motion( gc, T - U, 2 );
となる。
参考文献:小出昭一郎, "解析力学", 岩波書店
川谷亮治, "フリーソフトで学ぶ線形制御", 森北出版
(2010.12.5)
Topへ